Истечение газов через сужающиеся сопла (конфузоры)

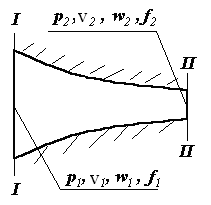
Рис. 2.12

На рис. 2.12 обозначены: р_i, v_i, w_i и f_i - давление, удельный объем, скорость газа в рассматриваемом сечении и площадь этого сечения. При i=1 указанные параметры соответствуют сечению I-I, а при i=2 - сечению II-II.

По отмеченной выше причине процесс течения газа через сопло предполагается адиабатным 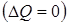. При допущении, что 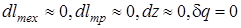и учитывая зависимость 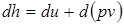, уравнение первого закона термодинамики для потока (2.36) можно представить в виде

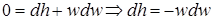. (2.46)

Беря интеграл с обеих частей последнего уравнения, находим

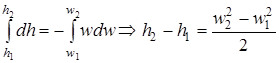. (2.47)

В силу имеющегося условия f₁>>f₂, w₂>>w₁, можно пренебречь 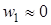и уравнению (2.47) придать вид

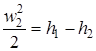. (2.48)

Из последнего выражения следует, что в конфузоре изменение кинетической энергии потока рабочего тела происходит лишь благодаря изменению его энтальпии.

Задача расчета конфузора сводится к определению w₂ при заданных значениях параметров р₁, v₁, р₂.

Перепишем уравнение (2.48) в виде

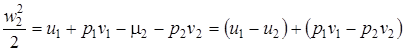. (2.49)

Исходя из первого закона термодинамики для адиабатного процесса 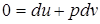, определяем значение первого слагаемого правой части
уравнения (2.49):

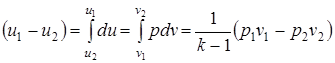. (2.50)

Найденное выражение подставляем в уравнение (2.49) и определяем w₂ – скорость истечения рабочего тела через сечение II - II

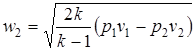. (2.51)

Далее используя формулу (2.51) для скорости и уравнение неразрывности для потока 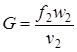, а также введя обозначение 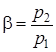, напишем соответствующие выражения для скорости потока и секундного массового расхода газа через сужающееся сопло в виде

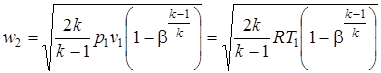, (2.52)

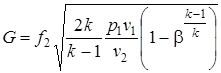. (2.53)

Учитывая, что течение через конфузор адиабатное, напишем выражение для удельного объема газа на выходе из сопла

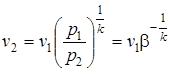. (2.54)

Подставив выражение (2.54) в формулу (2.53), находим

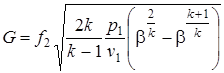. (2.55)

Рассматривая формулу (2.55) как функцию 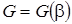, исследуем ее на экстремум. В результате находим критическое значение β_кр, при котором массовый расход газа через конфузор имеет максимальное значение

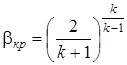. (2.56)

Подставив (2.56) в формулу (2.52), определяем максимально возможную скорость газа на выходе из конфузора:

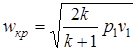, (2.57)

которую можно выразить еще через критические параметры состояния:

,

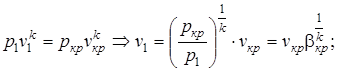
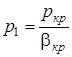тогда

, (2.58)

где 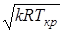- скорость распространения звуковых волн в идеальном газе.

Распределению скорости вдоль сопла соответствуют условия

для 1>β≥β_кр, 0<w₂<w_кр;

для β_кр>β>0, w₂=w_кр.

Формула (2.58) позволяет сделать вывод - скорость истечения из сужающегося сопла при критических условиях равна местной скорости звука. Поэтому скорость рабочего тела в конфузорах не может превышать скорости звука.

Выражение для максимального массового расхода через конфузор определяется путем подстановки выражения (2.56) в формулу (2.55)

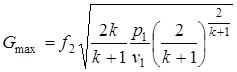. (2.59)

Как отмечалось выше, для получения сверхзвуковых скоростей необходимо использовать сопло Лаваля, в минимальном сечении которого скорость потока должна быть равна w_кр.

Расчет сужающейся части сопла Лаваля проводится точно так же, как и для обычного сужающегося дозвукового сопла. Площадь минимального сечения сопла определяется по заданному :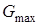

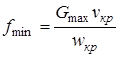, откуда диаметр этого сечения будет равен .

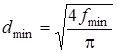Длину сужающейся части сопла Лаваля обычно принимают равной диаметру минимального сечения сопла

.

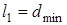Скорость на выходе из сопла Лаваля определяется формулой (2.52).

Площадь выходного сечения сопла Лаваля f₂ определяется из
уравнения (), соответственно диаметр этого сечения вычисляется из выражения 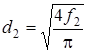. Длину расширяющейся части сопла l₂ вычисляют по формуле

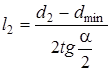, (2.60)

где α - угол конусности расширяющейся части сопла Лаваля (колеблется в пределах 8 - 10^о).

Вопросы для самопроверки

1. Получите выражение первого закона термодинамики для потока в термодинамической и механической формах.

2. Что такое работа проталкивания?

3. Запишите уравнение неразрывности потока в дифференциальной форме.

4. Что такое располагаемая работа?

5. Для осуществления каких процессов используют сопла и диффузоры?

6. В каких случаях процесс течения можно считать адиабатным?

7. Почему в сужающемся сопле нельзя превзойти скорость звука?

8. Как связано изменение площади поперечного сечения с измененем скорости и числом Маха?

9. В каких случаях необходимо использовать комбинированное сопло Лаваля?
10. При каких условиях режим течения в сопле Лаваля становится нерасчетным?

11. Как учитывается влияние трения на скорость течения газа или пара?

12. В чем сущность принципа обращения воздействия?

13. Что такое тепловое, механическое и расходное сопла?