Деление двоичных чисел

Деление двоичных чисел производится по тому же правилу, что и деление десятичных чисел. Как известно, при делении десятичных чисел делается вычитание из одного десятичного числа другого с использованием правила «заема» единиц в соседних, более старших разрядах.

Пример: 99 : 11 = 9 1100011 : 1011 = 1001

– 1011

0001011

– 1011

Преобразование целых чисел

Для преобразования целой части числа разделим левую и правую части полинома на основание q:

А_ц/q = a_n q^n-2 + a_n-1 q^n-3 +…a₂ q⁰ + a₁/q.

Выполняя последовательно операцию деления на q, получим новое целое число и остаток от деления с цифрой разряда a_n-1.

#₁ 100:8 = 12:8 =1; Ответ: 100 = 144₈.

4 4

#₂ 89:2 = 44:2 = 22:2 = 11:2 = 5:2 = 2:2 = 1:2; Ответ: 89:2 = 1011001

1 0 0 1 1 0 1

Для получения восьмеричного числа из двоичного числа нужно разбить его разряды на «триады»:

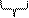
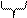
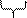
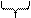А = 010 011 101 011 = 2353₈.

2 3 5 3

Для получения двоично-восьмеричного кода нужно каждую цифру восьмеричного числа заменить трёхразрядным двоичным числом:

2353₈ = 2·8² + 3·8¹ + 5·8⁰ = 128 +24 + 1.

В шестнадцатеричных числах основание q = 16; алфавит включает числа 0÷9 и буквы A÷F (10÷15).

Получение шестнадцатеричных чисел из двоичных

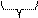
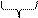
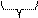
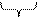
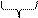A = 1101 1001 1110, 0001 0101 = D9E, 15₁₆.

D 9 E 1 5

Целую часть числа разбиваем на тетрады (четырех - разрядные числа), от запятой справа – налево, а дробную часть – тетрады, от запятой слева – направо. Полученные тетрады заменяем цифрами.