Основные свойства корней алгебраического уравнения
| Свойство 1 (о количестве корней алгебраического уравнения) |
Любое алгебраическое уравнение 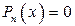 степени степени 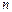 имеет на множестве комплексных чисел ровно имеет на множестве комплексных чисел ровно 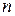 корней, если считать каждый корень столько раз, какова его кратность. корней, если считать каждый корень столько раз, какова его кратность.
|
Примеры (количество корней алгебраического уравнения)
1) x2 – 4x + 5 = 0 — алгебраическое уравнение второй степени (квадратное уравнение)
Þ 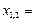 2 ±
2 ± 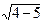 = 2 ± i — два корня;
= 2 ± i — два корня;
2) x3 + 1 = 0 — алгебраическое уравнение третьей степени (двучленное уравнение)
Þ 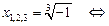
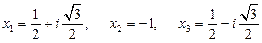 ;
;
3) P3(x) = x3 + x2 – x – 1 = 0 – алгебраическое уравнение третьей степени;
число x1 = 1 является его корнем, так как P3(1) 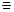 0, поэтому по теореме Безу
0, поэтому по теореме Безу 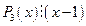 ; разделим многочлен P3(x) на двучлен (x – 1) «в столбик»:
; разделим многочлен P3(x) на двучлен (x – 1) «в столбик»:
| исходное уравнение P3(x) = x3 + x2 – x – 1 = 0 Û (x – 1)(x2 + 2x + 1) = 0 Û (x – 1)(x + 1)2 = 0 Þ x1 = 1 — простой корень, x2 = –1 — двукратный корень. |
| Свойство 2 (о комплексных корнях алгебраического уравнения с действительными коэффициентами) |
Если алгебраическое уравнение с действительными коэффициентами имеет комплексные корни, то эти корни всегда парные комплексно сопряженные, то есть если число 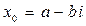 является корнем уравнения является корнем уравнения 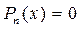 , то число , то число 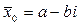 также является корнем этого уравнения. также является корнем этого уравнения.
|
w Для доказательства нужно использовать определение и следующие легко проверяемые свойства операции комплексного сопряжения:
если 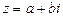 , то
, то 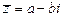 и справедливы равенства:
и справедливы равенства:
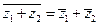 ,
, 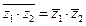 ,
, 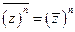 ,
, 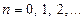 ,
,
если 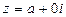 – действительное число, то
– действительное число, то 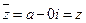 .
.
Так как 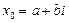 является корнем уравнения
является корнем уравнения 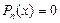 , то
, то 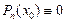
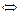
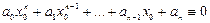 , где
, где 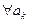 -- действительные числа при
-- действительные числа при 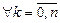 .
.
Возьмем сопряжение от обеих частей последнего равенства и используем перечисленные свойства операции сопряжения:
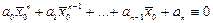
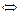
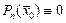 , то есть число
, то есть число 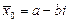 также удовлетворяет уравнению
также удовлетворяет уравнению 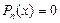 , следовательно, является его корнем. v
, следовательно, является его корнем. v
Например,
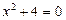
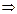
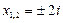 – парные комплексно сопряженные корни;
– парные комплексно сопряженные корни;
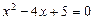
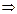
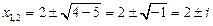 -парные компл. сопряженные корни.
-парные компл. сопряженные корни.
В качестве следствия из доказанного свойства о парности комплексных корней алгебраического уравнения с действительными коэффициентами получается ещё одно свойство многочленов.
| Свойство (о разложении целого многочлена с действительными коэффициентами на линейные и квадратичные множители) |
Любой алгебраический многочлен 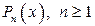 , имеющий только действительные коэффициенты, разлагается на произведение линейных и (или) квадратичных функций с действительными коэффициентами. , имеющий только действительные коэффициенты, разлагается на произведение линейных и (или) квадратичных функций с действительными коэффициентами.
|
w Будем исходить из разложения (6) многочлена 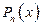 на линейные множители:
на линейные множители:
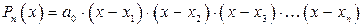 .
.
Пусть число x0 = a + bi — комплексный корень многочлена Pn(x), то есть это одно из чисел 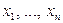 . Если все коэффициенты этого многочлена являются действительными числами, то число
. Если все коэффициенты этого многочлена являются действительными числами, то число 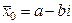 тоже является его корнем, то есть среди чисел
тоже является его корнем, то есть среди чисел 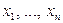 есть также число
есть также число 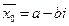 .
.
Вычислим произведение двучленов 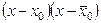 :
:
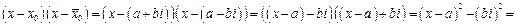
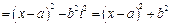 - получился квадратный трехчленс действительными коэф.
- получился квадратный трехчленс действительными коэф.
Таким образом, любая пара двучленов с комплексно сопряженными корнями в формуле (6) приводит к квадратному трехчлену с действительными коэффициентами. v
Примеры (разложение многочлена на множители с действительными коэф.)
1) P3(x) = x3 + 1 = (x + 1)(x2 – x + 1);
2) P4(x) = x4 – x3 + 4x2 – 4x = x(x –1)(x2 + 4).
| Свойство 3 (о целых и рациональных корнях алгебраического уравнения с действительными целыми коэффициентами) |
Пусть дано алгебраическое уравнение
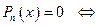 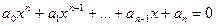 , все коэффициенты , все коэффициенты 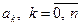 которого являются действительными целыми числами,
Если это уравнение имеет целый корень которого являются действительными целыми числами,
Если это уравнение имеет целый корень 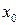 , то этот корень является делителем свободного члена , то этот корень является делителем свободного члена 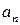 .
Если это уравнение имеет рациональный корень .
Если это уравнение имеет рациональный корень 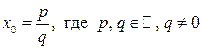 , то числитель , то числитель 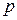 этого корня является делителем свободного члена этого корня является делителем свободного члена 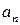 , а знаменатель , а знаменатель 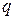 - делителем, отличным от единицы, старшего коэффициента - делителем, отличным от единицы, старшего коэффициента 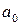 . .
|
w 1. Пусть целое число 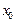 является корнем уравнения
является корнем уравнения 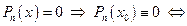
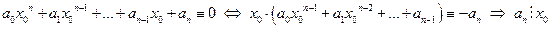 , так как целое чиисло
, так как целое чиисло 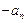 представлено произведением целого числа
представлено произведением целого числа 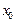 и выажения
и выажения 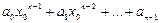 , имеющего целое значение.
, имеющего целое значение.
2. Пусть алгебраическое уравнение 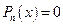 имеет рациональный корень
имеет рациональный корень
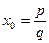 , причем, числа p и q являются взаимно простыми
, причем, числа p и q являются взаимно простыми 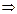
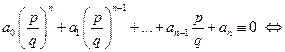
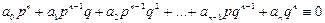 .
.
Это тождество можно записать в двух вариантах:
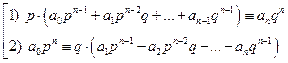
Из первого варианта записи следует , что 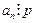 , а из второго – что
, а из второго – что 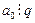 , так как числа p и q являются взаимно простыми. v
, так как числа p и q являются взаимно простыми. v
Примеры (подбор целых или рациональных корней алгебраического уравнения с целыми коэффициентами)
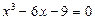 ;
;
если это кубическое уравнение имеет целый корень, то он находится среди делителей свободного члена уравнения, то есть среди делителей числа -9, образующих множество 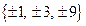 ; подставляя последовательно числа этого множества в исходное уравнение, находим, что
; подставляя последовательно числа этого множества в исходное уравнение, находим, что 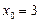 является корнем;
является корнем;
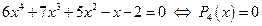 ;
;
если это уравнение 4-й степени имеет целые корни, то они находятся среди делителей свободного члена уравнения, то есть среди делителей числа -2, образующих множество чисел 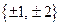 ; подставляем каждое из этих чисел в исходное уравнение:
; подставляем каждое из этих чисел в исходное уравнение:
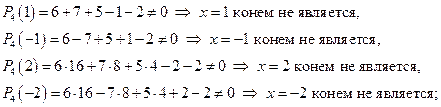
таким образом, показано, что целых корней данное уравнение не имеет.
Рациональный корень ищем в виде 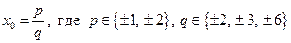 – это множество делителей, отличных от единицы, старшего коэффициента 6. Поэтому рациональный корень (если он существует) находится среди чисел множества
– это множество делителей, отличных от единицы, старшего коэффициента 6. Поэтому рациональный корень (если он существует) находится среди чисел множества 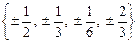 ; подстановкой каждому из этих чисел в исходное уравнение находим, что
; подстановкой каждому из этих чисел в исходное уравнение находим, что 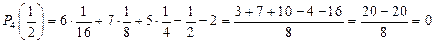 , следовательно, число
, следовательно, число 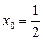 является корнем.
является корнем.
Дата добавления: 2021-07-22; просмотров: 492;