Основные определения

Целой алгебраической функцией или алгебраическим многочленом (полиномом)аргумента x называется функция следующего вида:

(1)

Здесь n – степень многочлена(натуральное число или 0),
x – переменная (действительная или комплексная),
a₀, a₁, …, a_n – коэффициенты многочлена(действительные или
комплексные числа),a₀ ¹ 0.

Например, ; ; , ;

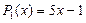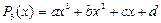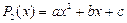, – квадратный трехчлен; .

Определение алгебраического уравнения -й степени

Уравнение называется алгебраическим уравнением n-й степениотносительно неизвестной x, если его левая часть является алгебраическим многочленом степени n относительно переменной x: Pn(x) = 0, (2)

Число х₀ такое, что P_n(x₀) º 0, называется нулем функцииP_n(x) или корнем уравнения .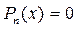

Например,

– алгебраическое уравнение первой степени, его корень ;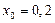

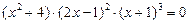– алгебраическое уравнение седьмой степени,

его корни , , .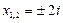

числа 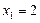и 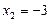являются нулями функции ,

так как и .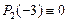

Замечание (к определению нулей целой алгебраической функции)

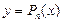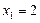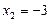В литературе часто нули функции называются ее корнями. Например, числа и называются корнями квадратичной функции .