Дифференцирующие цепи. Фильтр верхних частот.

Во многих радиотехнических устройствах используются простейшие цепи, выполняющие функцию дифференцирования или интегрирования входного сигнала, либо преобразующие спектральный состав этого сигнала. Цепи первого типа называются, соответственно, дифференцирующими и интегрирующими, а цепи второго типа называются фильтрами. К фильтрам относятся цепи, способные пропускать лишь сигналы определенного диапазона частот, и не пропускать (значительно ослаблять) сигналы не принадлежащие к этому диапазону. Если цепь пропускает все сигналы с частотами, меньшими некоторой граничной частоты f_гр, то ее называют фильтром нижних частот (ФНЧ). Цепь, пропускающую практически без ослабления все сигналы с частотами большими некоторой граничной частоты f_гр, называют фильтром верхних частот (ФВЧ). Кроме них существуют еще фильтры, пропускающие только сигналы, принадлежащие определенному частотному диапазону от f_гр1 до f_гр2 и ослабляющие сигналы всех частот 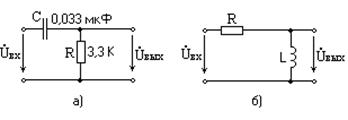f< f_гр1 и f > f_гр2. Такие фильтры называются полосовыми (ПФ).Фильтры, пропускающие сигналы всех частот, кроме заданного диапазона, ограниченного частотами f_гр1 и f_гр2, называются режекторными (заградительными).

Рис.3

На рис.3. показаны простейшие дифференцирующие цепи.

Коэффициент передачи цепи на рис.3,а равен:

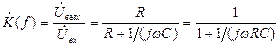(2.3)

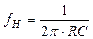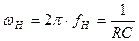Обозначим: и (2.4)

Тогда (2.3.) можно переписать:

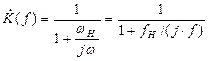(2.5)

Модуль коэффициента передачи напряжения:

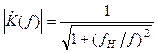(2.6)

При частоте 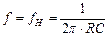активное сопротивление цепи R и реактивное 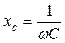равны и 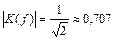, (2.7)

т.е. на этой частоте выходное напряжение по модулю в 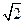раз меньше входного.

Для цепи на рис.3,б аналогично можно получить:

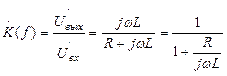(2.8)

Обозначив 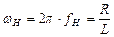или 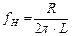, (2.9)

Выражение (2.8.) приведем к виду:

,

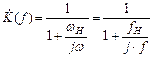который полностью совпадает с (2.5.). Поэтому и модуль коэффициента передачи напряжения будет определяться тоже соотношением (2.6). На частоте 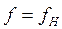, определяемой по (2.9) активное и реактивное сопротивления цепи также будут равны, следовательно, будет справедливо и соотношение (2.7).

Преобразуем выражение (2.5):

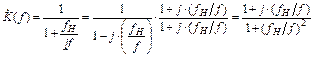(2.10)

Комплексный коэффициент передачи напряжения 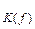, определяет соотношение не только амплитуд входного и выходного напряжений по формуле (2.6), но и сдвиг фазы между ними. Из (2.10) очевидно, что 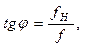откуда

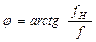(2.11)

Выражение (2.6.) определяет амплитудно – частотнуюхарактеристику (АЧХ), а (2.11.) – фазо – частотную характеристику (ФЧХ) дифференцирующих цепей. Вид этих характеристик представлен на рис.4.

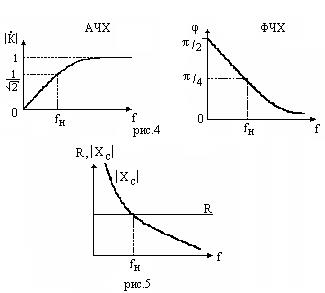
На частотах 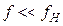, как следует из рис.5, представляющего собой частотную зависимость активного и реактивного сопротивлений цеп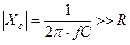и,

, и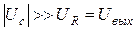

поэтому ток в цепи можно определить

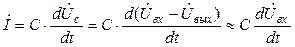
Выходное напряжение при этом условии 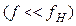будет

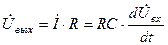(2.12)

Соотношение (2.12) показывает, что цепь рис.3,а действительно выполняет функцию дифференцирования входного напряжения, если выполняется условие .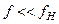

Аналогично, для цепи на рис.3,б можно показать, что при 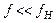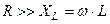. Поэтому ток в цепи 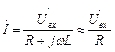, а выходное напряжение:

.

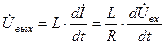T.е. цепь на рис.3,б тоже выполняет функцию дифференцирования входного напряжения при том же условии .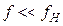

Тот факт, что представленные схемы одновременно являются фильтрами верхних частот, наглядно иллюстрирует график АЧХ на рис.4. Граничными частотами любого фильтра называются частоты, на которых выходное напряжение по модулю уменьшается до значения 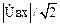. Из графика АЧХ видно, что при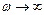 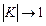, а на частоте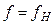 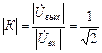, т.е. 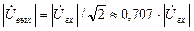. Таким образом, частота f_Н, определяемая формулами (2.4) и (2.9), является граничной частотой для фильтров верхних частот, представленных на рис.3,а и 3,б.