Расчет передачи на тяговую способность.

Основным расчетом ременных передач является расчет на его тяговую способность (проектный расчет).

Тяговая способность ремня характеризуется экспериментальными кривыми скольжения (рис.10), которые строят следующим образом:

- по оси ординат откладывают относительное скольжение ремня ξ, %, и КПД передачи η, %,

- по оси абсцисс - коэффициент тяги передачи φ=F_t/(2F₀), который представляет собой относительную нагрузку передачи.

С ростом нагрузки упругое скольжение ремня увеличивается по закону прямой линии, при этом значительно увеличивается КПД передачи. Эта закономерность наблюдается до так называемого критического значения коэффициента тяга φ_к, соответствующего наибольшей допускаемой нагрузке на ремень. С увеличением нагрузки свыше допустимой дополнительно возникает проскальзывание ремня и суммарное скольжение быстро возрастает (появляется частичное буксование), сопровождаясь резким падением КПД передачи. При предельном значении φ=φ_max, наступает полное буксование (проскальзывание) ремня. Из кривых скольжения и КПД следует, что лучшая тяговая способность ремня соответствует критическому значению коэффициента тяги φ_к. Экспериментально установлено, что в среднем для плоских ремней φ_к=0,4...0,6, для клиновых ремней φ_к=0,7...0,9.

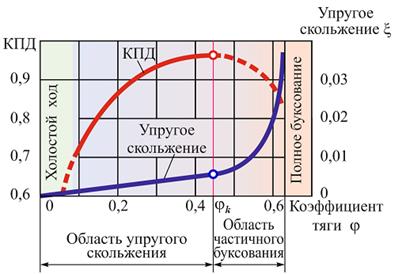
Рис.10. Кривые скольжения и КПД

Расчет плоских ремней по тяговой способности производят по допускаемому полезному напряжению k.

Полезное напряжение ремня k 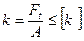(16)

Так как ,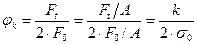

то, следовательно .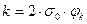

Расчетное допускаемое полезное напряжение для плоского ремня

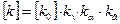, (17)

где 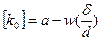- допускаемое (приведенное) полезное напряжение,

аи w — коэффициенты, выражаемые в единицах напряжения; δ— толщина ремня; d — диаметр меньшего шкива.

k_v - скоростной коэффициент, учитывающий ослабление сцепления ремня со шкивом под действием центробежной силы

k_α- коэффициент, учитывающий влияние угла обхвата меньшего шкива;

k_в - коэффициент, учитывающий вид передачи и ее расположение.

1 2 34

Дата добавления: 2017-05-02; просмотров: 1348;