Расчет зубьев на изгиб (проверочный расчет)

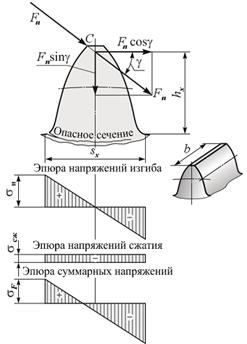Напряжения изгиба наиболее опасны у ножки зуба (рис. 7). При расчете зубьев на прочность по напряжениям изгиба вводят следующие допущения:

- нагрузка передаётся одной парой зубьев и приложена к вершине зуба.

- зуб рассматриваем как консольную балку, для которой справедлива гипотеза плоских сечений.

Действующие силы:

- сила нормального давления в точке контакта зубьев ;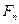

- окружная сила .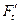

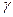- угол направления нормальной силы. Угол несколько 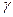больше угла :

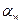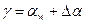
Перенесём силу 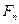на ось симметрии зуба и разложим её на составляющие:

;

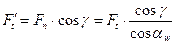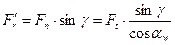
Рис.7

Напряжение изгиба в опасном сечении, расположенном вблизи хорды основной окружности:

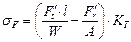(10)

где 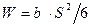- момент сопротивления; 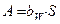- площадь;

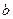- ширина зубчатого венца; 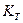- теоретический коэффициент концентрации напряжений.

За расчётные напряжения принимают растягивающие напряжения, так как в большинстве случаев усталостные трещины возникают здесь. Размерные величины 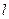и 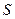неудобные для расчета. Так как зубья различного модуля геометрически подобны, то величины 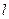и 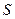выражают через безразмерные величины:

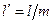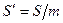и , где 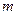- модуль зубьев.

Подставим ввыражение (10) для расчёта напряжений изгиба в опасном сечении значения всех составляющих. Получим:

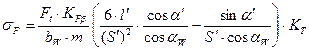, (11)

где 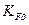- коэффициент неравномерности нагрузки.

Введём обозначение: 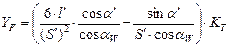- коэффициент формы зуба. Величина 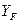зависит от числа зубьев и коэффициента смещения исходного контура и определяется по специальным графикам. С учётом этих обозначений условие прочности на изгиб запишется:

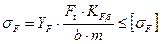(12)

Полученная формула (12) является основной для проверочного расчёта прямозубой передачи.

Косозубые и шевронные передачи рассчитываются аналогично прямозубым. Однако, ввиду того что прочность косозубых и шевронных передач выше, чем прямозубых, в расчетные формулы вводятся коэффициенты повышения прочности.