Шейкерная (перемешиванием) сортировка

12 3

Рассматриваемый в данной статье алгоритм имеет несколько непохожих друг на друга названий. Среди них: сортировка перемешиванием, двунаправленная пузырьковая сортировка, шейкерная сортировка, пульсирующая сортировка (ripple sort), трансфертная сортировка (shuttle sort), и даже сортировка «счастливый час» (happy hour sort). Второй вариант (двунаправленная пузырьковая сортировка) наиболее точно описывает процесс работы алгоритма. Здесь, в его название, довольно-таки удачно включен термин «пузырьковая». Это действительно альтернативная версия известного метода, модификации в котором заключаются, по большей части, в реализации, упомянутой в названии, двунаправленности: алгоритм перемещается, ни как в обменной (пузырьковой) сортировке – строго снизу вверх (слева направо), а сначала снизу вверх, потом сверху вниз.

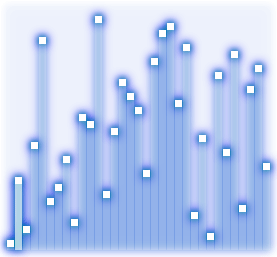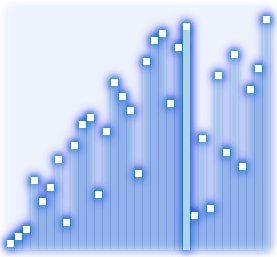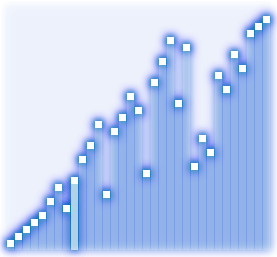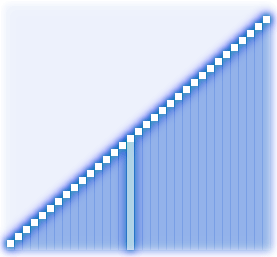
Перестановка элементов в шейкерной сортировке выполняется аналогично той же в пузырьковой сортировке, т. е. два соседних элемента, при необходимости, меняются местами. Пусть массив требуется упорядочить по возрастанию. Обозначим каждый пройденный путь от начала до конца последовательности через W_i, где i – номер пути; а обратный путь (от конца к началу) через -W_j, где j – номер пути. Тогда после выполнения W_i, один из неустановленных элементов будет помещен в позицию справа, как наибольший из еще неотсортированных элементов, а после выполнения -W_j, наименьший из неотсортированных, переместиться в некоторую позицию слева. Так, например, после выполнения W₁в конце массива окажется элемент, имеющий наибольшее значение, а после -W₁ в начало отправиться элемент с наименьшим значением.

Код программы на C++:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41

#include "stdafx.h"#include <iostream> using namespace std; //функция обмена void Swap(int *Mas, int i) { int temp; temp=Mas[i]; Mas[i]=Mas[i-1]; Mas[i-1]=temp; } //функция шейкерной сортировки void ShakerSort(int *Mas, int Start, int N) { int Left, Right, i; Left=Start; Right=N-1; while (Left<=Right) { for (i=Right; i>=Left; i--) if (Mas[i-1]>Mas[i]) Swap(Mas, i); Left++; for (i=Left; i<=Right; i++) if (Mas[i-1]>Mas[i]) Swap(Mas, i); Right--; } } //главная функция void main() { setlocale(LC_ALL,"Rus"); int n, k; cout<<"Размер массива > "; cin>>n; int *A=new int[n]; for (k=0; k<n; k++) { cout<<k+1<<" элемент > "; cin>>A[k]; } ShakerSort(A, 1, n); cout<<"Результирующий массив: "; for (k=0; k<n; k++)cout<<" "<<A[k]; system("pause>>void"); }

Следующая таблица отражает временную сложность алгоритма шейкерной сортировки для трех случаев.

Лучший случай	Средний случай	Наихудший случай
O(n)	O(n²)	O(n²)

Приведенные временные показатели не позволяют рекомендовать алгоритм для использования его в практических целях. В обучении, ввиду своей относительной сложности, метод, несомненно, будет полезен.

Быстрая сортировка

Выбирая алгоритм сортировки для практических целей, программист, вполне вероятно, остановиться на методе, называемом «Быстрая сортировка» (также «qsort» от англ. quick sort). Его разработал в 1960 году английский ученый Чарльз Хоар, занимавшийся тогда в МГУ машинным переводом. Алгоритм, по принципу функционирования, входит в класс обменных сортировок (сортировка перемешиванием, пузырьковая сортировка и др.), выделяясь при этом высокой скоростью работы.

Отличительной особенностью быстрой сортировки является операция разбиения массива на две части относительно опорного элемента. Например, если последовательность требуется упорядочить по возрастанию, то в левую часть будут помещены все элементы, значения которых меньше значения опорного элемента, а в правую элементы, чьи значения больше или равны опорному. Вне зависимости от того, какой элемент выбран в качестве опорного, массив будет отсортирован, но все же наиболее удачным считается ситуация, когда по обеим сторонам от опорного элемента оказывается примерно равное количество элементов. Если длина какой-то из получившихся в результате разбиения частей превышает один элемент, то для нее нужно рекурсивно выполнить упорядочивание, т. е. повторно запустить алгоритм на каждом из отрезков.

Таким образом, алгоритм быстрой сортировки включает в себя два основных этапа:

· разбиение массива относительно опорного элемента;

· рекурсивная сортировка каждой части массива.

Разбиение массива

Еще раз об опорном элементе. Его выбор не влияет на результат, и поэтому может пасть на произвольный элемент. Тем не менее, как было замечено выше, наибольшая эффективность алгоритма достигается при выборе опорного элемента, делящего последовательность на равные или примерно равные части. Но, как правило, из-за нехватки информации не представляется возможности наверняка определить такой элемент, поэтому зачастую приходиться выбирать опорный элемент случайным образом.

В следующих пяти пунктах описана общая схема разбиения массива (сортировка по возрастанию):

1. вводятся указатели first и last для обозначения начального и конечного элементов последовательности, а также опорный элемент mid;

2. вычисляется значение опорного элемента (first+last)/2, и заноситься в переменную mid;

3. указатель first смещается с шагом в 1 элемент к концу массива до тех пор, пока Mas[first]>mid. А указатель last смещается от конца массива к его началу, пока Mas[last]<mid;

4. каждые два найденных элемента меняются местами;

5. пункты 3 и 4 выполняются до тех пор, пока first<last.

После разбиения последовательности следует проверить условие на необходимость дальнейшего продолжения сортировки его частей. Этот этап будет рассмотрен позже, а сейчас на конкретном примере выполним разбиение массива.

Имеется массив целых чисел Mas, состоящий из 8 элементов (рис. 5.5): Mas[1..8]. Начальным значением first будет 1, а last – 8. Пройденная часть закрашивается голубым цветом.

В качестве опорного элемента возьмем элемент со значением 5, и индексом 4. Его мы вычислили, используя выражение (first+last)/2, отбросив дробную часть. Теперь mid=5.

Первый элемент левой части сравнивается с mid. Mas[1]>mid, следовательно firstостается равным 1. Далее, элементы правой части сравниваются с mid. Проверяется элемент с индексом 8 и значением 8. Mas[8]>mid, следовательно lastсмещается на одну позицию влево. Mas[7]<mid, следовательно last остается равным 7. На данный момент first=1, а last=7. Первый и седьмой элементы меняются местами. Оба указателя смещаются на одну позицию каждый в своем направлении.

Алгоритм снова переходит к сравнению элементов. Второй элемент сравнивается с опорным: Mas[2]>mid, следовательно first остается равным 2. Далее, элементы правой части сравниваются с mid. Проверяется элемент с индексом 6 и значением 1: Mas[6]<mid, следовательно last не изменяет своей позиции. На данный моментfirst=2, а last=6. Второй и шестой элементы меняются местами. Оба указателя смещаются на одну позицию каждый в своем направлении.

Алгоритм снова переходит к сравнению элементов. Третий элемент сравнивается с опорным: Mas[3]<mid, следовательно first смещается на одну позицию вправо. Далее, элементы правой части сравниваются с mid. Проверяется элемент с индексом 5 и значением 9: Mas[5]>mid, следовательно last смещается на одну позицию влево. Теперь first=last=4, а значит, условие first<last не выполняется, этап разбиения завершается.

На этом этап разбиения закончен. Массив разделен на две части относительно опорного элемента. Осталось произвести рекурсивное упорядочивание его частей.

12 3

Дата добавления: 2017-05-02; просмотров: 3070;