Основные сведения о моделях и моделировании.
Моделирование как средство научного исследования.
В познании мира человек часто прибегает к моделированию. Модели необходимы для изучения структуры объекта, его основных свойств, законов развития, взаимосвязи с окружающим миром, способов управления и возможности прогнозирования последствии реализации заданных способов воздействия на объект, а также определения оптимальных параметров с целью снижения затрат производства, получения максимального эффекта. Хорошо построенная модель, как правило, дает возможность получить новые знания об объекте-оригинале.
Цели и задачи моделирования:
Оптимальное проектирование новых и совершенствование действующих технологических процессов.
Получение и обработка необходимой информации о ходе технологического процесса с целью прогнозирования поведения изучаемого объекта, управления и регулирования параметрами процесса.
Решение задач исследования объектов, где невозможно проводить активные эксперименты - режимы работы нового технологического оборудования.
Максимальное ускорение переноса результатов лабораторных исследований в промышленные масштабы.
Модель - это представление процесса или объекта, которое лучше помогает понять его характеристики, устройство и функционирование. Модели значительно облегчают познание системы, позволяют проводить исследование в абстрактном плане, прогнозировать поведение системы, упрощать задачи, анализировать системы.
Основные сведения о моделях и моделировании.
Классификацию моделей можно проводить по разным типам признаков:
· по способу познания: нaучно-технические, художественные, житейские.
· по природе моделей: предметные (физические, материальные), знаковые (мысленные).
Существует значительное количество моделей, из них нижеследующие представляют интерес для технологических процессов хлебопекарного, макаронного и кондитерского производств.
Описательные модели - словесное описание исследуемого процесса или объекта. Формализация описательной модели осуществляется по определенным правилам (в виде анкеты, вопросника и т.д.). Эти модели - простые, самые грубые и неточные.
Графические модели обеспечивают более полное представление о реальном объекте. Они дают изображение его внешнего вида или внутреннего устройства в статике (на фотографии или рисунке), или запись на графопостроителе или дисплее в динамике.
Математическая модель – один из видов моделирования, когда поставленная задача математически строго описана. Математическая модель является упрощенным представлением реального объекта, его адекватным описанием в сжатой форме. Она определяет зависимости между параметрами реальной системы или объекта в виде некоторых математических соотношений. Формализация экспериментальных данных - это построение по ним зависимости, описывающей исследуемый процесс.
В рамках изучения научно-технических моделей практический интерес представляют математические модели технологических процессов. В табл. 1 показаны виды математических моделей по различным признакам классификации.
1. Классификация математических моделей
| Признаки классификации | Виды математических моделей |
| 1. Принадлежность к иерархическому уровню | 1. Модели микроуровня 2. Модели макроуровня 3. Модели метауровня |
| 2. Характер отображаемых свойств объекта | 1. Структурные 2. Функциональные |
| 3. Способ представления свойств объекта | 1. Аналитические 2. Алгоритмические 3. Имитационные |
| 4. Способ получения модели | 1. Теоретические 2. Эмпирические |
| 5. Особенности поведения объекта | 1. Детерминированные 2. Вероятностные |
Приведенная классификация математических моделей может быть применена по отношению к любым объектам. Рассмотрим особенности различных видов моделей применительно к объектам (процессам) хлебопекарного, макаронного и кондитерского производств.
Выделяют несколько иерархических уровней математических моделей. Уровень моделирования определяется величиной неделимого объекта, при переходе к более высокому уровню значение этой величины возрастает.
Математические моделипроизводственного процесса на микроуровнехарактеризуют ограниченные местные явления, отражают физические, химические, микробиологические, коллоидные процессы, протекающие, например, при созревании теста.
Математические моделипроизводственного процесса на макроуровне описывают технологические процессы в целом.
Математические моделипроизводственного процесса на метауровне описывают технологические системы (участки, цехи, предприятие в целом).Макромодели и метамодели применяются для описания в целом крупных объектов, общих управленческих и экономико-социальных структур, например таких, как общенациональная валовая продукция и др.
Микромодели допустимы в рамках одного предприятия или отрасли промышленности.
В зависимости от характера отображаемых свойств объекта модели классифицируются на структурные и функциональные.
Структурные математические модели предназначены для отображения структурных свойств объектов. Например, в системе автоматизированного проектирования технологических процессов (САПР ТП) хлебопекарного, макаронного и кондитерского производств для представления структуры технологического процесса, расцеховки изделий используется структурно – логические модели.
Функциональные математические модели предназначены для отображения информационных, физических, временных процессов, протекающих в работающем оборудовании, в ходе выполнения технологических процессов и т.д.
По способу представления свойств объекта различают аналитические, алгоритмические и имитационные модели.
Аналитические математические модели представляют собой математические выражения выходных параметров как функций от параметров входных.
Аналитическое моделирование основано на косвенном описании моделируемого объекта с помощью набора математических формул. Аналитические модели являются эффективным инструментом для решения задач оптимизации процессов, протекающих в технологических системах, а также оптимизации и вычисления характеристик самих технологических систем.
Алгоритмические математические модели выражают связи между выходными параметрами и параметрами входными и внутренними в виде алгоритма.
Имитационные математические модели – это алгоритмические модели, отражающие развитие процесса (поведение исследуемого объекта) во времени при задании внешних воздействий на процесс (объект). Например, это модели систем массового обслуживания, заданные в алгоритмической форме.
Имитационное моделирование основано на прямом описании моделируемого объекта. Существенной характеристикой таких моделей является структурное подобие объекта и модели. Это значит, что каждому существенному с точки зрения решаемой задачи элементу объекта ставится в соответствие элемент модели. При построении имитационной модели описываются законы функционирования каждого элемента объекта и связи между ними.
Работа с имитационной моделью заключается в проведении имитационного эксперимента. Процесс, протекающий в модели в ходе эксперимента, подобен процессу в реальном объекте. Поэтому исследование объекта на его имитационной модели сводится к изучению характеристик процесса, протекающего в ходе эксперимента.
Ценным качеством имитации является возможность управлять масштабом времени. Динамический процесс в имитационной модели протекает в так называемом системном времени. Системное время имитирует реальное время. При этом пересчет системного времени в модели можно выполнять двумя способами. Первый способ заключается в «движении» по времени с некоторым постоянным шагом. Второй способ заключается в «движении» по времени от события к событию, при этом считается, что в промежутках времени между событиями в модели изменений не происходит.
Теоретические математические модели создаются в результате исследования объектов (процессов) на теоретическом уровне. Например, существуют выражения для сил резания, полученные на основе обобщения физических законов. Но они не приемлемы для практического использования, т.к. очень громоздки и не совсем адаптированы к реальным процессам обработки материалов.
Эмпирические математические модели создаются в результате проведения экспериментов (изучения внешних проявлений свойств объекта с помощью измерения его параметров на входе и выходе) и обработки их результатов методами математической статистики.
Детерминированные математические модели описывают поведение объекта с позиций полной определенности в настоящем и будущем. Примеры таких моделей: формулы физических законов, технологические процессы обработки деталей и т.д.
Вероятностные математические модели учитывают влияние случайных факторов на поведение объекта, т.е. оценивают его будущее с позиций вероятности тех или иных событий. Примеры таких моделей: описание ожидаемых длин очередей в системах массового обслуживания, ожидаемых объемов выпуска сверхплановой продукции производственным участком, точности размеров в партии деталей с учетом явления рассеяния и т.д.
Создание математической модели - это важная и ответственная часть исследования, требующая глубокого знания не только математики, но и существа моделируемых явлений. Модель должна отражать закономерности реальных процессов. Например, физико-химические закономерности при превращении веществ можно описать уравнениями баланса или кинетическими уравнениями.
Непредсказуемые изменения, которые происходят при неизменности условий, в которых производится измерение параметров объекта, объясняются случайностью. Например, случайными являются хаотичные колебания показателей качества готовых изделий (выпускаемых на одном и том же оборудовании) относительно оптимального значения, характеристик качества основного и дополнительного сырья хлебопекарного производства, стабильности работы оборудования, параметров технологического процесса. Причиной случайной изменчивости является наличие в природе неконтролируемых факторов, проявление которых неодинаково в каждом измерении (имеет место случайное событие) и которые заранее не могут быть учтены.
Различают три класса математических моделей: детерминированные, стохастические и комбинированные.
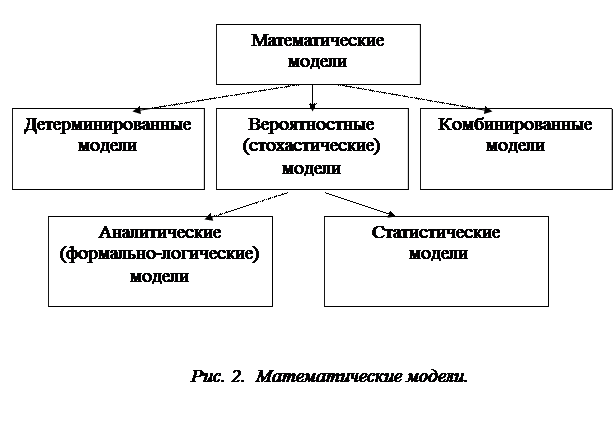
Для описания функционирования объекта, когда исходные данные полностью известны и достоверны, а случайные факторы пренебрежимо малы (можно считать, что все измерения производятся точно), используются детерминированные модели.
К классу детерминированных моделей относятся модели, в которых каждому фиксированному сочетанию входных переменных соответствует одно или несколько вполне определенных сочетаний выходных переменных. Примерами детерминированных моделей могут служить модели производственных процессов, построенных на основе известных физико-химических соотношений или формализованных связей.
Если при измерениях хотя бы некоторых параметров наблюдаются случайные компоненты, то такие объекты описываются вероятностными (стохастическими) моделями.
Для стохастических моделей характерно соответствие фиксированному сочетанию входных переменных некоторой плотности вероятностного распределения выходных параметров. Модели второго класса отражают случайную природу моделируемого объекта. В этом случае значение выходных переменных оказывается случайными, распределенными по статистическому закону, параметры которого зависят от сочетания значений входных переменных.
Вероятностные модели могут быть аналитическими или статистическими.
Статистические модели позволяют учитывать все многообразие связей и факторов, оказывающих влияние на исследуемые объекты. Их получение не требует значительных средств: объект рассматривается как "черный ящик", а реальные взаимосвязи аппроксимируются некоторыми зависимостями. Однако найденными зависимостями можно уверенно пользоваться лишь для той области значений параметров, в которой проводились наблюдения, не допуская экстраполяцию на новые данные.
К статистическим математическим моделям относятся модели законов распределения вероятностей, а также модели, описывающие структуру (линейную или нелинейную) и параметры взаимосвязей между признаками объекта: модели регрессии, дисперсионного анализа, анализа временных рядов и другие.
Различают параметрические (либо сводящиеся к параметрическим) методы для исследования статистических моделей, когда может быть получено аналитическое описание законов распределения вероятностей признаков объекта. В статистике их также называют классическими или гауссовскими методами. И непараметрические методы - когда заданы лишь различия между распределениями. Непараметрические методы требуют меньшего объема исходной информации и являются менее чувствительными к возможным искажениям реальных данных (робастными). Большее практическое применение получили ранговые непараметрические методы.
Одним из возможных видов комбинированной модели можно представить себе детерминированную модель производственного процесса, в которой несколько коэффициентов определяются известной плотностью вероятностного распределения.
На практике, при работе или исследовании объекта, присутствуют обе составляющие - закономерная, которая может быть описана уравнением, и случайная (шум, помехи, случайный разброс значений). Выявить существующие закономерности можно лишь при многократном наблюдении ряда случайных факторов, выполняемом в однотипных условиях.
Независимо от принадлежности к определенному классу модель должна отвечать одному основному требованию - быть адекватной моделируемому процессу (объекту) в заданной области. Следует подчеркнуть, что моделей абсолютно адекватных объектам не существует. Удовлетворительной модель считается в том случае, если она описывает процесс с ошибкой, не превышающей заданную.
В отличие от реально поставленного эксперимента математическая модель имеет ряд преимуществ. Во-первых, это экономия материальных ресурсов, требуемых для постановки и проведения физического эксперимента; во-вторых, возможность апробации системы в экстремальных условиях и даже за их пределами; в-третьих, оценка работоспособности системы с длительными технологическими циклами в существенно более сжатые сроки.
Математическая модель по форме представляет собой систему дифференциальных уравнений в частных производных, описывающих поведение объекта в окружающей среде с установленными граничными условиями. Так как даже для известных уравнений точные решения могут быть получены только для отдельных частных случаев, математическое моделирование означает выполнение следующих основных этапов:
-формулировку математической модели объекта, сопоставимой с имеющимися или прогнозируемыми экспериментальными данными, включая разработку методов, построения такой модели при недостатке исходной информации;
-разработку методов решения соответствующей математической задачи и их реализацию в программах для ЭВМ;
-проведение в рамках принятой модели математического эксперимента;
-обработка и анализ полученных результатов.
Дата добавления: 2021-07-22; просмотров: 1031;











