Работа и мощность электрического тока.

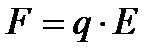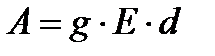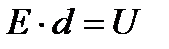Для поддержания электрического тока в проводниках в них должно существовать электрическое поле, которое совершает положительную работу, передвигая заряды вдоль проводника. Если напряженность электрического поля в проводнике Е, то на заряд q действует сила . Пусть заряд переместился по проводнику на расстояние d. Тогда электрический ток совершит работу равную . Но , где U-разность потенциалов на концах проводника и, следовательно, работа .

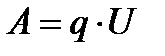При движении зарядов работа электрического тока в проводнике за время t равна количеству электричества Q, протекшему через поперечное сечение проводника за это время, умноженному на разность потенциалов между концами проводника U:

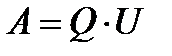
Поскольку ток 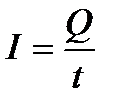, то 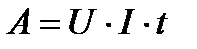, а работа за единицу времени, т.е. мощность .

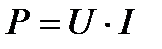Единица измерения мощности называется ватт.

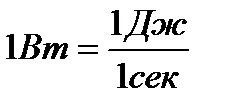, 1 кВт=10³ Вт.

Электрическая энергия подсчитывается в ватт-часах 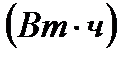или .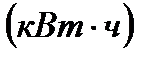

Расчет электрических цепей постоянного тока.

Правила Кирхгофа.

1) Сумма токов, направленных к точке разветвления, равна сумме токов, направленных от нее.

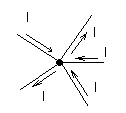I₁+I₃+I₅=I₂+I₄

Преобразуя это соотношение, получим:

I₁+(-I₂)+I₃+(-I₄)+I₅=0

Т.е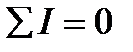
т.е. алгебраическая сумма токов в точке разветвления равна нулю.

При этом токи, направленные к узлу, считаются положительными, а токи, направленные от узла – отрицательными (или наоборот).

Узлом называют точку цепи из которой провода уходят больше чем в двух направлениях

Второе правило Кирхгофа:

В замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжения в отдельных сопротивлениях.

При этом положительными надо считать ЭДС, направления которых совпадают с произвольно выбранным направлением обхода по контуру.

Если контур не содержит источников, то .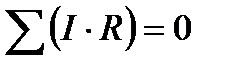

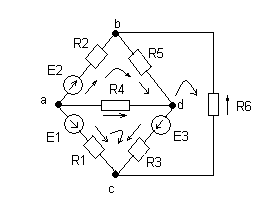
Пример: Решение задачи методом непосредственного применения законов Кирхгофа.

Дано:

Е₁=30 В; Е₂=20 В; Е₃=15 В.

R₁=4 Ом; R₂=2 Ом; R₃=1 Ом; R₄=10 Ом; R₅=6 Ом; R₆=3 Ом.

Решение:

1-е правило – число узловых уравнений должно быть на единицу меньше числа узлов электрической цепи.

2-е правило – недостающие уравнения составляются по второму Кирхгофа; при этом нужно выбирать наиболее простые контуры (с меньшим числом источников ЭДС и сопротивлений) в таком порядке, чтобы в каждом новом контуре содержалась, по меньшей мере, одна ветвь, не входившая в контуры, для которых уже составлены уравнения.

Решение

1.Составим уравнения по первому закону Кирхгофа, т.к. в схеме четыре узла, то можем составить (4-1)=3 уравнения.

Узел «а» -I₂ - I₁ - I₄ = 0

Узел «в» I₂ + I₆ - I₅ = 0

Узел «с» I₁ + I₃ - I₆ = 0

2. Составляем недостающие уравнения по второму закону Кирхгофа (для решения системы с 6-ю неизвестными необходимо 6 уравнений).

Контур «aвda» : I₂R₂ + I₅R₅ – I₄R₄ = E₂

Контур «adca» : I₄R₄ + I₃R₃ – I₁R₁ = E₃ – E₁

Контур «abR₆ca» : I₂R₂ – I₆R₆ – I₁R₁ = E₂ – E₁

Подставив значения E и R, получим систему уравнений:

- I₂ – I₁- I₄ = 0

I₂ + I₆ – I₅ = 0

I₁ + I₃ – I₆ = 0

2I₂ + 6I₅ – 10I₄ = 20

10I₄ + I₃ – 4I₁ = 15 – 30

2I₂ – 3I₆ – 4I₁ = 20 – 30

Далее решаем полученную систему уравнений любым возможным способом (можно на ЭВМ).

Решив систему уравнений, получим:

I₁ = 1.18 A; I₂ = - 0.1 A; I₃ = 0.5 A; I₄ = -1 A; I₅ = 1.57 A; I₆ = 1.68 A.

Решение системы уравнений, для сложной цепи, требует значительной затраты времени, поэтому можно использовать более простые методы.