Круговые процессы (циклы)
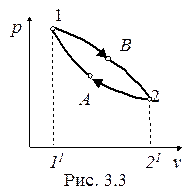 | 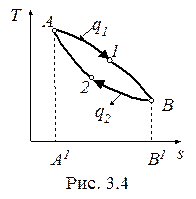 | ||
В тепловом двигателе рабочее тело совершает замкнутый процесс (цикл) в направлении движения часовой стрелки (рис. 3.3 и 3.4).
На участке 1-B -2 (рис. 3.3) происходит расширение рабочего тела, на участке 2 - А -1 – его сжатие.
Работа процесса расширения (полученная работа) равна
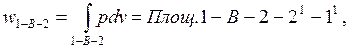
работа процесса сжатия (затраченная работа) равна
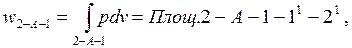
результирующая (полезная) работа равна
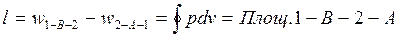 .
.
На участке A-1-B (рис. 3.4) осуществляется процесс подвода теплоты к рабочему телу, а на участке B-2 - A – ее отвод.
Подведенная теплота в цикле равна
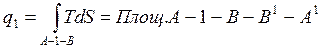 ,
,
отведенная теплота равна
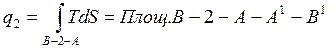 .
.
Разность подведенной и отведенной теплот превращается в работу
 ,
,
и она характеризуется площадью цикла в T – s- диаграмме.
Таким образом, в p-v- и T-s- диаграммах площадь цикла является работой теплового двигателя.
Такой же результат получается с использованием математического выражения первого закона термодинамики для замкнутого процесса (цикла). Выполняя интегрирование по замкнутому контуру, имеем
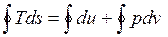 .
.
Поскольку 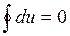 , следовательно,
, следовательно,
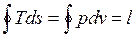 .
.
3.3.1. Цикл Карно
Термическим коэффициентом полезного действия (КПД) цикла называется отношение работы, произведенной двигателем за цикл, к количеству теплоты, подведенной за этот же цикл:
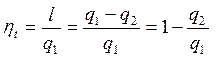 . .
| (3.5) |
Термический КПД характеризует степень термодинамического совершенства обратимых циклов.
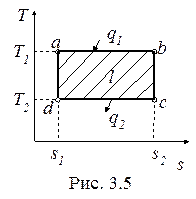 Цикл Карно - это обратимый цикл, который имеет максимальный термический КПД среди всех циклов, осуществляемых в данном интервале температур горячего и холодного источников тепла. Он состоит из двух адиабатных процессов сжатия и расширения рабочего тела (da и bc, рис. 3.5) и двух изотермических процессов подвода и отвода теплоты (ab и cd).
Цикл Карно - это обратимый цикл, который имеет максимальный термический КПД среди всех циклов, осуществляемых в данном интервале температур горячего и холодного источников тепла. Он состоит из двух адиабатных процессов сжатия и расширения рабочего тела (da и bc, рис. 3.5) и двух изотермических процессов подвода и отвода теплоты (ab и cd).
Подводимая теплота в цикле
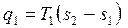 , ,
| (3.6) |
отводимая теплота
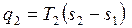 , ,
| (3.7) |
где T1 – температура горячего источника, T2 – температура холодного источника.
Согласно (3.5), (3.6) и (3.7) термический КПД цикла Карно равен
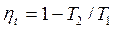 , ,
| (3.8) |
он не зависит от свойств рабочего тела, а определяется только температурами горячего и холодного источников тепла. Поскольку T2 > 0 и T1 < µ, то ht < 1.
3.4. Понятия средних термодинамических температур
подвода и отвода тепла
На рис. 3.6 представлен произвольный обратимый цикл 1-a-2-b в T-s- диаграмме.
Подводимая теплота в цикле (q1) характеризуется площадью c-1-a-2-d и может быть заменена площадью равновеликого прямоугольника c-3-4-d. Таким образом,
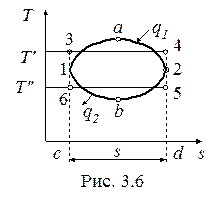 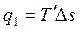 , ,
| (3.9) |
где 
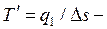 средняя термодинамическая температура подвода теплоты в произвольном обратимом цикле.
средняя термодинамическая температура подвода теплоты в произвольном обратимом цикле.
Аналогично отводимая теплота равна
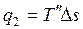 , ,
| (3.10) |
где 
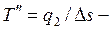 средняя термодинамическая температура отвода теплоты.
средняя термодинамическая температура отвода теплоты.
Подстановка (3.9) и (3.10) в (3.5) дает
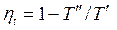 . .
| (3.11) |
Таким образом, термический КПД произвольного обратимого цикла всегда может быть вычислен через средние термодинамические температуры подвода и отвода теплоты. Из формулы (3.11) следует: чем выше 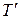 , или, чем ниже
, или, чем ниже 
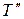 , тем больше термический КПД цикла.
, тем больше термический КПД цикла.
Эксергия теплоты
Эксергией теплоты, переданной от горячего источника тепла с температурой T к рабочему телу, называется максимальная работа, которая может быть получена за счет этой теплоты при условии, что холодным источником является окружающая среда с температурой Tоc.
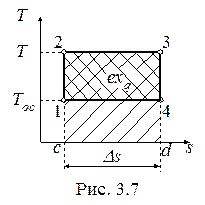 Максимальную работу (рис. 3.7) можно получить, если осуществить цикл Карно (1-2-3-4) в данном интервале температур T-Tоc .
Максимальную работу (рис. 3.7) можно получить, если осуществить цикл Карно (1-2-3-4) в данном интервале температур T-Tоc .
Теплота, воспринятая рабочим телом от горячего источника, равна

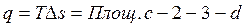 .
.
Эксергия теплоты вычисляется следующим образом:

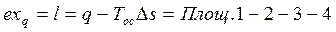 ,
,
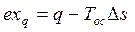
| (3.12) |
где 
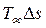 - анергия, непревратимая в работу часть теплоты.
- анергия, непревратимая в работу часть теплоты.
Термический КПД цикла Карно равен
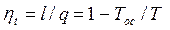 , ,
|
откуда
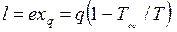 . .
| (3.13) |
Таким образом, эксергия теплоты, полученной от источника теплоты с постоянной температурой T, может быть раcсчитана по формулам (3.12) и (3.13).
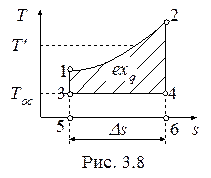 В том случае, когда источник теплоты имеет переменную температуру (рис. 3.8) (например, горение топлива происходит при постоянном давлении с увеличением T), применимы формулы (3.12) и (3.14):
В том случае, когда источник теплоты имеет переменную температуру (рис. 3.8) (например, горение топлива происходит при постоянном давлении с увеличением T), применимы формулы (3.12) и (3.14):
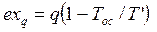 , (3.14)
, (3.14)
где 
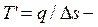 средняя термодинамическая температура подвода теплоты в процессе 1-2.
средняя термодинамическая температура подвода теплоты в процессе 1-2.
При передаче теплоты от тела с более высокой температурой к телу с более низкой температурой (внешний необратимый процесс) эксергия теплоты уменьшается.
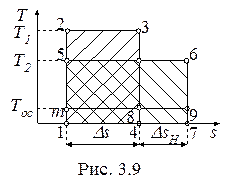 Пусть (рис. 3.9) теплота q передается от тела с температурой T1 к телу с температурой T2. Переданная теплота характеризуется одинаковыми площадями в T-s- диаграмме:
Пусть (рис. 3.9) теплота q передается от тела с температурой T1 к телу с температурой T2. Переданная теплота характеризуется одинаковыми площадями в T-s- диаграмме:
q = Площ.1-2-3-4 = Площ.1-5-6-7. Эксергия теплоты уменьшилась (Площ. m-5-6-9 < Площ. m-2-3-8) на величину потерянной эксергии (Площ. 4 – 8 –9 -7).
Таким образом, потеря эксергии составляет
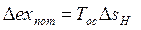 , ,
| (3.15) |
где DsH –увеличение энтропии от необратимости процесса теплообмена.
Уравнение (3.15), которое называют уравнением Гюи - Стодолы, имеет важное значение, т.к. характеризует потерю эксергии любых необратимых процессов.
Дата добавления: 2021-07-22; просмотров: 514;











