Математическое выражение первого закона термодинамики
Вся подводимая к рабочему телу теплота расходуется на изменение внутренней энергии и на совершение работы:
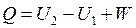 , Дж, , Дж,
| (2.8) |
 Дж/кг Дж/кг
| (2.9) |
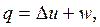
| (2.10) |
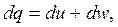
| (2.11) |
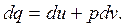
| (2.12) |
Формулы (2.8) – (2.12) математически выражают первый закон термодинамики через внутреннюю энергию.
Подстановка 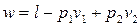
 в (2.9) дает
в (2.9) дает
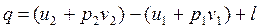 , ,
|
где u + pv = h , Дж / кг – удельная энтальпия, является параметром состояния
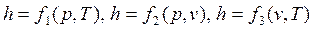 . .
|
Энтальпия идеального газа зависит только от температуры
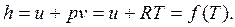
|
При количественном анализе процессов часто используется математическая запись первого закона термодинамики через энтальпию:
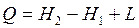 , Дж, , Дж,
| (2.13) |
 , Дж / кг, , Дж / кг,
| (2.14) |
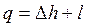 , ,
| (2.15) |
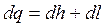 , ,
| (2.16) |
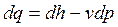 . .
| (2.17) |
Теплоемкость газов
Теплоемкость – это количество тепла, которое необходимо подвести к единице количества вещества, чтобы нагреть его на 10.
Различают теплоемкости:
· массовую (c, Дж/кг×К), отнесенную к одному килограмму газа;
· объемную (c¢¢, Дж/м3×К), отнесенную к одному м3 объема при нормальных физических условиях;
· мольную (mс, Дж/кмоль×К), отнесенную к 1 киломолю газа,
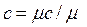 , , 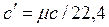 , , 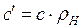 , ,
|
где rН - плотность газа при нормальных физических условиях (p=760 мм рт. ст., t = 00 С).
Согласно определению теплоемкости
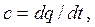
| (2.18) |
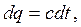
| (2.19) |
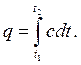
| (2.20) |
Теплоемкость реальных газов зависит от давления и от температуры 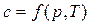 .
.
Теплоемкость идеальных газов (кроме одноатомного) зависит только от температуры 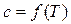 .
.
Теплоемкость одноатомного идеального газа постоянна (c = const).
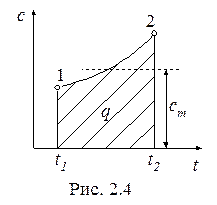 Для газов, теплоемкость которых зависит от температуры, различают истинную и среднюю теплоемкость. Формула (2.18) определяет теплоемкость при данной температуре – истинную теплоемкость.
Для газов, теплоемкость которых зависит от температуры, различают истинную и среднюю теплоемкость. Формула (2.18) определяет теплоемкость при данной температуре – истинную теплоемкость.
На рис. 2.4 показана зависимость теплоемкости газа от температуры (1-2).
Исходя из геометрического смысла интеграла, можно записать:
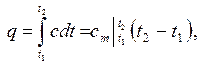
где 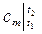 - средняя теплоемкость газа для интервала температур t1 – t2, которая может быть вычислена по одной из формул:
- средняя теплоемкость газа для интервала температур t1 – t2, которая может быть вычислена по одной из формул:
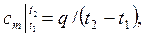
| (2.21) |
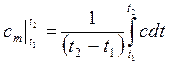 . .
| (2.22) |
Среднюю теплоемкость 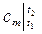 можно рассчитать:
можно рассчитать:
– по результатам эксперимента, используя формулу (2.21);
– по формуле (2.22), используя зависимость теплоемкости от температуры, например,
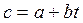 или или 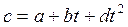 , ,
|
где a, b, d – постоянные величины;
– через средние теплоемкости 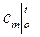 :
:
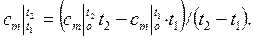
| (2.23) |
Для воздуха таблица средних теплоемкостей 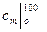 ,
, 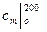 и т.д. дана в Приложении.
и т.д. дана в Приложении.
Изменение температуры газа при одном и том же количестве сообщаемой теплоты зависит от характера процесса подвода теплоты, поэтому теплоемкость является функцией процесса:
– в изобарных процессах - изобарная теплоемкость 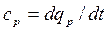 ;
;
– в изохорных - изохорная 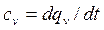 ;
;
– в изотермических - 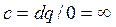 ;
;
– в адиабатных - 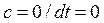 ;
;
– в политропных - 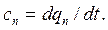

Связь изохорной и изобарной теплоемкостей для идеального газа описывает уравнение Майера
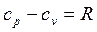 , Дж/(кг×К), , Дж/(кг×К),
| (2.24) |
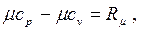 Дж/(кмоль×К). Дж/(кмоль×К).
| (2.25) |
Отношение теплоемкостей cp/cv  называется показателем адиабаты или коэффициентом Пуассона.
называется показателем адиабаты или коэффициентом Пуассона.
Для идеального газа
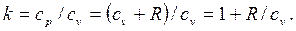
| |
| Отсюда | |
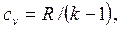
| (2.26) |
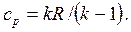
| (2.27) |
Молекулярно-кинетическая теория теплоемкости, основанная на допущении о равномерном распределении энергии по степеням свободы молекул и не учитывающая энергию внутримолекулярных колебаний, дает следующие значения мольных теплоемкостей:
- для одноатомных газов 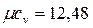 кДж/(кмоль×К);
кДж/(кмоль×К);
- для двухатомных газов  кДж/(кмоль×К);
кДж/(кмоль×К);
- для трех– и многоатомных газов 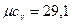 кДж/(кмоль×К).
кДж/(кмоль×К).
В одноатомных газах отсутствуют внутримолекулярные колебания и постоянное значение теплоемкости, не зависящее от температуры ( 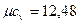 кДж/(кмоль×К)), подтверждается экспериментальными данными. Теплоемкости остальных газов зависят от температуры, и указанные значения теплоемкости подтверждаются экспериментальными данными только в области комнатных температур.
кДж/(кмоль×К)), подтверждается экспериментальными данными. Теплоемкости остальных газов зависят от температуры, и указанные значения теплоемкости подтверждаются экспериментальными данными только в области комнатных температур.
Энергию колебательного движения атомов в молекуле учитывает квантовая теория теплоемкости. Значения теплоемкостей для двух- , трех- и многоатомных газов, рассчитанные по формуле Эйнштейна, подтверждаются экспериментом и приводятся в справочниках.
Теплоемкость газовой смеси рассчитывается по формулам:
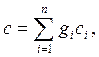 Дж/(кг×К), Дж/(кг×К),
| (2.28) |
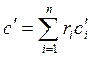 , Дж/(м3×К), , Дж/(м3×К),
| (2.29) |
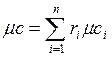 , Дж/(кмоль×К). , Дж/(кмоль×К).
| (2.30) |
Методические указания. Вопросы и задачи
1. Обратите внимание на следующее:
а) параметры:
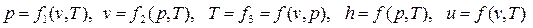
- это функции состояния, и их изменение (Dp, Dv, DT, Dh, Du) не зависит от характера процесса;
б) работа (l, w), теплоемкость (с) являются функциями процесса и зависят от характера процесса;
в) энтальпия, внутренняя энергия, теплоемкость идеального газа зависят только от температуры: 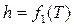 ;
; 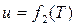 ;
; 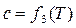 ;
;
г) теплоемкость одноатомного идеального газа не зависит от температуры (с = const).
2. Уясните физический смысл внутренней энергии (u) и энтальпии (h) рабочего тела, работы изменения объема (w) и внешней работы (l).
3. Можно ли утверждать, что математическое выражение первого закона термодинамики через внутреннюю энергию справедливо для закрытых термодинамических систем, а через энтальпию – для открытых?
4. Давление газа в изохорном процессе при v = 0,5 м3/кг уменьшилось от p1 = 6 бар до р2 = 1 бар.
Определите работу изменения объема (w) и внешнюю работу (l) указанного процесса. Представьте процесс в p – v- диаграмме и покажите соответствующие этим работам площади.
5. Для изотермического процесса идеального газа дано: 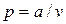 , где
, где
a = const; p1 = 10 бар, v1 = 0,5 м3/кг, р2 = 1 бар.
Определите внешнюю работу (l), изменение энтальпии (Dh), теплоту процесса (q).
Решение
Внешняя работа изотермического процесса, согласно (2.7) и уравнению 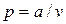 , равна
, равна

|
Постоянная 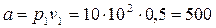 , кПа.м3/кг
, кПа.м3/кг
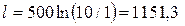 кДж/кг
кДж/кг
Изменение энтальпии идеального газа в изотермическом процессе Dh= 0. Теплота изотермического процесса q = l согласно (2.15)
Ответы: l = q = 1151,3кДж/кг Dh = 0.
6. Температура воздуха увеличилась от t1 = 300 C до t2 = 1500 C.
Определите, на сколько изменение энтальпии (Dh) воздуха отличается от изменения внутренней энергии (Du). Принять, что воздух – идеальный газ.
7. Рассчитайте изохорную и изобарную теплоемкости гелия, отнесенные к одному килограмму газа. Мольная масса гелия m = 4 кг/кмоль.
8. Определите среднюю мольную изобарную теплоемкость водорода в интервале температур 400 – 600 0С, если истинная теплоемкость описывается формулой
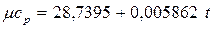 , кДж/(кмоль×0С).
, кДж/(кмоль×0С).
9. Определите массовую теплоемкость (ср) генераторного газа, если его объемный состав 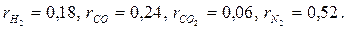
Примечание. Теплоемкость компонентов принять постоянной согласно молекулярно-кинетической теории газов.
Решение
В соответствии с молекулярно-кинетической теорией газов мольная изохорная теплоемкость углекислого газа (СО2) mсv = 29,1 кДж/(кмоль×К), двухатомных газов (H2, CO, N2) mсv = 20,8 кДж/(кмоль×К),.
Мольные изобарные теплоемкости, согласно (2.25) для двухатомных газов:
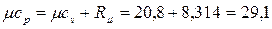 кДж/(кмоль×К),
кДж/(кмоль×К),
для СО2
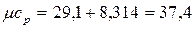 кДж/(кмоль×К).
кДж/(кмоль×К).
Согласно (2.30) мольная изобарная теплоемкость газовой смеси
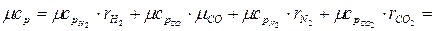
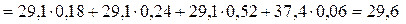 кДж/(кмоль.К)
кДж/(кмоль.К)
Согласно (1.15) мольная масса генераторного газа
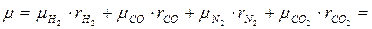
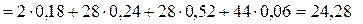 кг/кмоль.
кг/кмоль.
Массовая изобарная теплоемкость генераторного газа
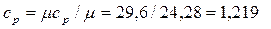 кДж/(кг.К).
кДж/(кг.К).
Ответ: 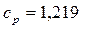 кДж/(кг.К).
кДж/(кг.К).
10. Рассчитайте среднюю изобарную теплоемкость воздуха, отнесенную к 1 кг, в интервале температур 700 – 900 0С, используя табличные значения теплоемкостей 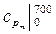 и
и 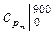 (см. Приложение).
(см. Приложение).
Ответы
3. Да. 4. l = 250 кДж/кг, w = 0. 6. 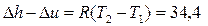 кДж/кг.
кДж/кг.
7. 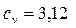 кДж/(кг.К),
кДж/(кг.К), 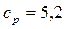 кДж/(кг.К).
кДж/(кг.К).
8. 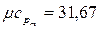 кДж/(кмоль.К). 10.
кДж/(кмоль.К). 10. 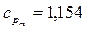 кДж/(кг.К).
кДж/(кг.К).
Дата добавления: 2021-07-22; просмотров: 652;











