Электромеханические свойства двигателя постоянного тока независимого возбуждения (ДПТ НВ)

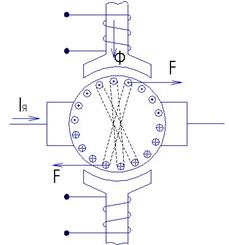
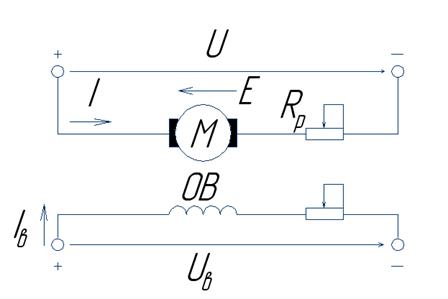Обычная схема включения двигателя постоянного тока независимого возбуждения представлена на рис. 1. Якорь двигателя М и его обмотка возбуждения ОВ обычно получают питание от разных, независимых друг от друга источников (преобразователей) напряжения U и Uв, что позволяет отдельно регулировать напряжение на якоре двигателя и на обмотке возбуждения и выполнять их на разное номинальное напряжение. Лишь при наличии сети постоянного тока или при нерегулируемом преобразователе в якорной цепи обмотка возбуждения питается от того же источника напряжения, что и якорь двигателя. Но и в этом случае ток возбуждения I_в не зависит от тока I якоря двигателя.

Направления тока I и ЭДС вращения двигателя Е, показанные на рис. 1, соответствуют двигательному режиму работы, когда электрическая энергия потребляется двигателем из сети (от источника напряжения U) и преобразуется в механическую энергию, мощность которой равна Р = Мω. Зависимость же между М и ω двигателя определяется его механической характеристикой.

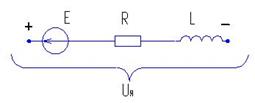
Аналитическое выражение механической характеристики двигателя может быть получено из уравнения равновесия напряжений, составленного для якорной цепи схемы (рис. 1). При установившемся режиме работы двигателя приложенное напряжение U, В, уравновешивается падением напряжения в якорной цепи IR и наведенной в якоре ЭДС вращения Е, В, т. е.

U = IR + E, ( 1)

здесь I — ток в якорной цепи двигателя, A; R — суммарное сопротивление якорной цепи, Ом, включающее внешнее сопротивление резистора Rp и внутреннее сопротивле­ние якоря двигателя Rя (при наличии дополнительных полюсов учитывается и их сопротивление);

E=cФω, (2)

где c — коэффициент, зависящий от конструктивных данных двигателя, c = pN/2na (p — число пар полюсов двигателя; N — число активных проводников . обмотки якоря; а — число пар параллельных ветвей обмотки якоря); Ф и ω — соответственно магнитный поток, Вб, и угловая скорость двигателя, рад/с.

Если в (1) вместо Е подставим ее значение Е из (2), то получим уравнение для скорости двигателя

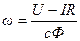, (3)

Уравнение (3) представляет собой зависимость скорости двигателя от тока якоря. Такую зависимость называют электромеханической характеристикой двигателя.

Электрическая схема замещения (с учетом противоЭДС)

Р _эл = U_dI_я > 0

R – активное сопротивление обмотки;

L – индуктивность якорной цепи.

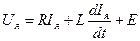
Полная система уравнений, описывающих ДПТ НВ:

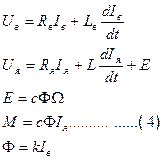
Уравнение движения привода: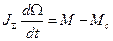

Для получения уравнения механической характеристики необходимо подставить (3) значение тока I, найденное из (4), получим выражение для механической характеристики:

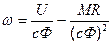(5)

или

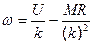(6)

где

k=сФ (7)

Коэффициент k принимается постоянным, не зависящим от нагрузки, если у двигателя с независимым возбуждением имеется компенсационная обмотка. Он может считаться неизменным, если для обычных двигателей пренебречь реакцией якоря.

Из (5) видно, что механическая характеристика двигателя ω=f(М) при неизменных параметрах U, Ф и R представляется прямой линией.

На рис. 2 представлены механические характеристики двигателя независимого возбуждения для различных сопротивлений якорной цепи. Как видно из (5), при М = 0 все характеристики проходят через одну точку, лежащую на оси ординат. Угловая скорость в этой точке имеет вполне определенное значение, не зависящее от сопротивления якорной цепи. Эта скорость носит название скорости идеального холостого хода и определяется выражением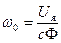

При скорости идеального холостого хода, когда ток в якорной цепи равен нулю, ЭДС якоря, направленная навстречу приложенному напряжению, равна ему по абсолютному значению. Если двигатель до приложения нагрузки работал с угловой скоростью ω₀, то при появлении на его валу момента сопротивления угловая скорость будет снижаться. Следствием этого будет уменьшение ЭДС вращения Е согласно (2) и увеличение тока якоря в соответствии с (1) и момента двигателя по (4). Угловая скорость будет снижаться до тех пор, пока момент двигателя не сравняется с моментом сопротивления. Разность значений установившихся скоростей электропривода до и после приложения заданной статической нагрузки называется статическим падением (перепадом) скорости электропривода. Второй член (6) характеризует собой статическое падение угловой скорости (перепад) относительно угловой скорости идеального холостого хода:

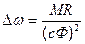
Таким образом, уравнение для скорости двигателя может быть записано так:

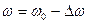
Верхняя характеристика из семейства, приведенного на рис.2 называется естественной. Естественной характеристикой называется такая характеристика двигателя, которая получается при отсутствии внешних резисторов в якорной цепи и номинальных значениях напряжения и магнитного потока двигателя.

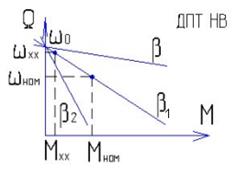
М_хх – момент холостого хода;

w_хх – скорость холостого хода;

М_ном – номинальный момент.

М_хх@0,05М_ном.

Естественная характеристика самая жесткая (соответствует b). При уменьшении b возрастает Dw, то есть характеристика менее жесткая (соответствует b₁, b₂).

М_кз может формироваться лишь аварийно, при прямом пуске двигателя: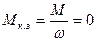

w=0 точка короткого замыкания. М_кз=(10…20)М_ном. Такой режим не допустим даже кратковременно, М_к.з.>>λМ_ном

Физические ограничения М_доп:

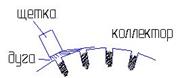
Длина дуги пропорциональна квадрату тока: ℓ_дуги»I_я².

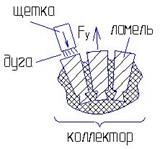При М_кз дуга перекрывает промежуток между щетками двигателя, что соответствует короткому замыканию (это называется перекрытием коллектора или круговым огнем по коллектору и, как следствие, двигатель выходит из строя).

Реальная перегрузочная способность ДПТ .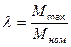

l≤2…2,5 – превышение можно допускать лишь на очень короткий срок.

Но существуют специальные серии двигателей с полым якорем, с печатным якорем, которые допускают перегрузки до l=5…7.

Ламели изготовляются из меди.

2.2. 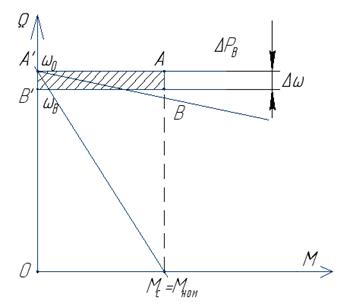Энергетика ДПТ НВ.

Потери в двигателе пропорциональны снижению скорости Δω под действием нагрузки М_с

Докажем это утверждение.

Пусть двигатель работает под нагрузкой М_с=М_ном на механической характеристике А'В.

Рабочая точка В. Оценим потери в двигателе.

Отдаваемая механическая мощность (см. рис):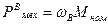

Потребляемая из сети электромагнитная мощность:

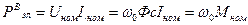
Здесь использовано: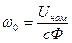

Потери в двигателе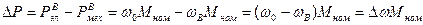

В масштабе рисунка, механическая мощность равна площади прямоугольника В'ВСО:

,

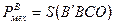а соответственно, потребляемая мощность и потери:

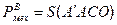
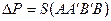
Площадь потерь заштрихована на рисунке.

Таким образом, потери ΔР тем больше, чем больше просадка скорости Δω=АВ под нагрузкой относительно скорости идеального холостого хода. Этими представлениями будем пользоваться для сопоставления энергетики различных способов регулирования скорости двигателя.

Самая плохая энергетика – точка С:

Р_мех=w_с∙М_ном=0.

Вся потребляемая энергия переводится в тепло. Р_эл=U_ном∙I _ном.

Чем мягче характеристика двигателя, тем больше в нем внутренние потери.