Доказательство совершенной стойкости шифра Вернама по конечному модулю

Теоретическая стойкость, совершенно стойкий шифр

Теоретико-информационный подход к оценке стойкости шифров в 1949 году предложил американский инженер К.Шеннон. На основе вероятностной модели шифра он сформулировал понятие совершенно стойкого шифра и показал, что Вернама на основе случайной равновероятной гаммы удовлетворяет требованию совершенной стойкости.

Хотя конечной целью дешифрования является восстановление открытого текста или ключа шифрования, даже возможность угадывания открытого текста с некоторой вероятностью может быть полезна атакующей стороне. Для коммерческих сделок сумма тендерного предложения, «угаданная» по порядку величины может сыграть решающую роль.

Например, перехватив сообщение {АБВВГ…}, зашифрованное простой заменой, злоумышленник получит информацию о совпадении третьего и четвертого символов в открытом тексте, что делает весьма вероятным предположение об открытом тексте {СУММА…}. После чего он может попытаться отождествить последующий шифрованный текст с тем или иным числовым выражением стоимости сделки.

Сказанное позволяет сделать вывод, что для надежного шифра перехват шифрованного сообщения не должен изменять представления о допустимом содержании открытого текста.

Шифр называется совершенно стойким по Шеннону, если открытый и шифрованный тексты статистически независимы, то есть для " M,C в случае P(C)>0 имеет место равенство условной и безусловной вероятности:

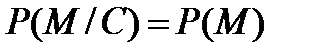
Иначе говоря, перехват шифрованного сообщения (криптограммы) не увеличивает объема информации об открытом тексте, если ключ шифрования неизвестен. При этом распределения вероятностей на множестве открытых текстов до и после перехвата шифрованного сообщения (апостериорное и априорное распределение) совпадают.

Доказательство совершенной стойкости шифра Вернама по конечному модулю

Теорема.Шифр Вернама по модулю N:

является совершенно стойким шифром, если ключ шифрования Г ={g₁ …g_n } является результатом случайного равновероятного выбора из множества всех возможных n-грамм 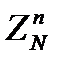в алфавите Z_N.

Доказательство:Пусть имеем открытый и шифрованный тексты M,CÎ 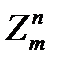, причем вероятность P(M)>0. Так как ключ Г выбирается случайно и равновероятно, то P(Г)=N^-n.

Для заданных текстов M и C ключ Г из уравнения (1) определяется однозначно, поэтому:

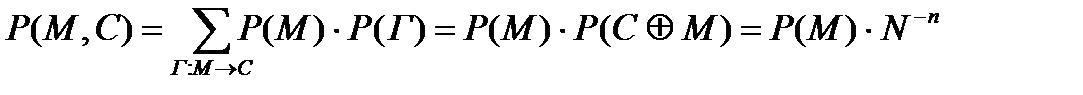
где CÅM означает поразрядное сложение по mod N двух n-мерных векторов.

Откуда, используя определение условной вероятности, получим:

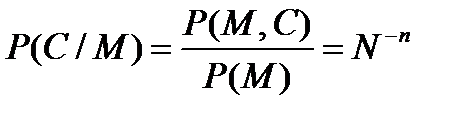
По формуле Байеса для P(C)>0 из последнего равенства следует:

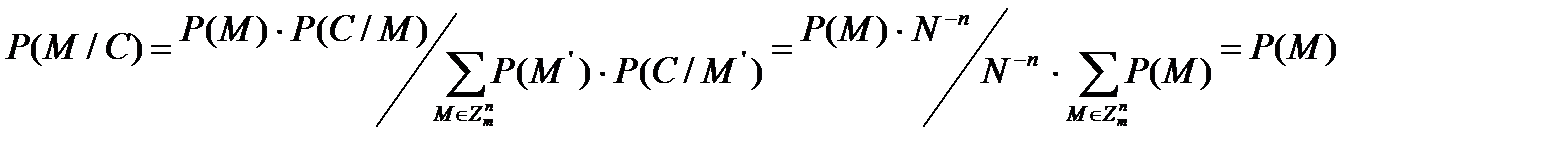
Что и требовалось доказать.