Уравнение аддитивности термических сопротивлений.
Определим количество тепла, передаваемого в единицу времени от более нагретого теплоносителя 
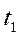 к менее нагретому
к менее нагретому 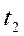 через многослойную стенку (рис. 2) при установившемся процессе. Предположим, что стенка состоит из двух слоев: первого слоя толщиной
через многослойную стенку (рис. 2) при установившемся процессе. Предположим, что стенка состоит из двух слоев: первого слоя толщиной 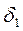 и теплопроводностью
и теплопроводностью 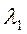 и второго слоя толщиной
и второго слоя толщиной 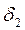 и теплопроводностью
и теплопроводностью
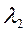 .
.
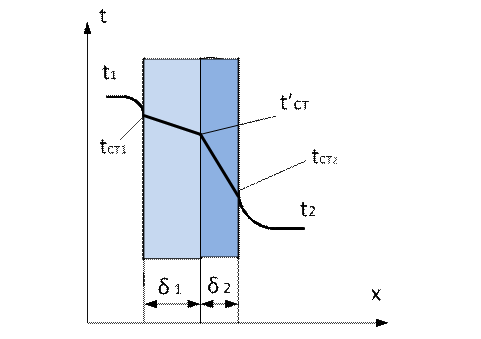
Рис.2. Профиль температур при переносе тепла через многослойную стенку.
Температуры по поверхности со стороны более и менее нагретых теплоносителей постоянны. Поверхность теплопередачи F.
Количество тепла, передаваемого от более нагретого теплоносителя к стенке за период времени 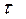 равно:
равно:
Q= 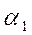 F
F 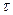
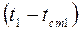
То же самое количество тепла передается посредством теплопроводности через каждую стенку:
Q= 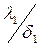 F
F 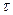
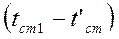
Q= 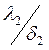 F
F 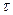
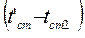
Количество тепла, отдаваемого стенкой менее нагретому теплоносителю за период времени 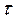 :
:
Q= 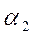 F
F 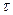
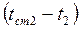
Из представленных уравнений выразим термические сопротивления:
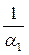 =
= 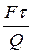
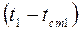
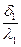 =
= 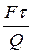
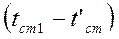
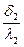 =
= 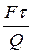
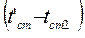
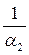 =
= 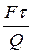
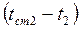
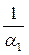 и
и 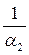 - термические сопротивления более нагретой и менее нагретой сред;
- термические сопротивления более нагретой и менее нагретой сред;
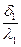 и
и 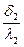 - термические сопротивления стенок.
- термические сопротивления стенок.
Сложим полученные уравнения и представим их относительно теплового потока Q:
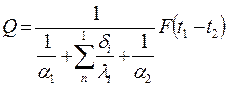

Сравним полученное уравнение с основным уравнением теплопередачи:
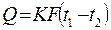 , где K – коэффициент теплопередачи;
, где K – коэффициент теплопередачи;
Получим: 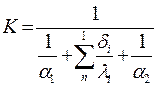 , где
, где 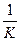 - общее термическое сопротивление R.
- общее термическое сопротивление R.
Полученное уравнение называют уравнением аддитивности термических сопротивлений.
Дата добавления: 2021-07-22; просмотров: 594;











