Минимизация с помощью карт Карно
Карта Карно представляет собой прямоугольную таблицу, в которой число клеток равно 2 в степени n. Карта заполняется на основе таблицы истинности или записи логической функции в ДСНФ.
Для приведенного выше примера таблица истинности имеет вид, представленный на рис. 111. Внутри карты Карно записываются значения логической функции. Значения входных переменных записываются по краям карты. Каждая входная переменная делит поле карты пополам. Для одной половинки поля значения входных переменных равны 1, для другой - 0. При расстановке переменных необходимо соблюдать следующее правило:
соседние столбцы и строки должны различаться только одной переменной. Значение входной переменной, равное 1, принято охватывать скобочкой.
Там, где нет скобочки, значение переменной равно 0. Возможно другое обозначение переменной по краю Карты (рис. 112).
Далее единицы в карте Карно объединяются контурами. Правила нанесения контуров:
1. Каждый контур должен быть прямоугольным.
2. Количество клеток внутри контура должно быть равным 2 в степени n,
где n=1,2,3,...
3. Одни и те же клетки с единицами могут входить в несколько контуров.
4. Размеры контуров должны быть как можно большими, а число контуров
как можно меньшим.
5. Нижняя и верхняя строки, левый и правый столбцы считаются соседними.
Запись минимизированного выражения по карте Карно с нанесенными контурами выполняется по следующим правилам:
1. Количество слагаемых в дизъюнктивной форме равно количеству контуров.
2. Из конъюнкции переменных исчезают те переменные, границы изменения которых пересекаются контуром.
Для рассматриваемого примера:
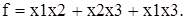
 |
В этом выражении x1x2 записано из первого контура, x2x3 - из второго контура, x1x3 - из третьего контура.
Реализация по этому выражению имеет вид, представленный на рис.
113. Реализация требует два корпуса микросхем.
Для уменьшения количества корпусов преобразуют полученную логическую функцию по законам Моргана и записывают её в базисе И-НЕ или в базисе ИЛИ-НЕ. Применение законов Моргана позволяет избавиться от “+” в логической функции или от произведений. Один из законов Моргана имеет вид:
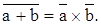
Дата добавления: 2021-07-22; просмотров: 410;











