Примеры задач линейного программирования

Задача об использовании ресурсов.Для изготовления двух видов продукции 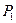и и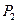спользуется четыре вида ресурсов 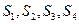, Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице 1:

Вид ресурса	Запас ресурса	Число единиц ресурсов, затрачиваемых на изготовление единицы продукции
		-
			-

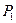
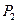
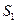
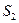
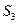
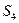
Прибыль, получаемая от единиц продукци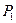и и 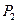-соответственно 2 и 3 руб. Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.

Решение. Составим экономико-математическую модель задачи. Пусть 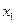и 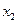- число единиц продукци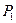и и 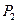соответственно, запланированных к производству. Для их изготовления потребуется 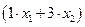единиц ресурса 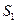; 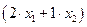единиц ресурса 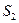; 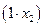единиц ресурса 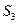и 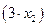единиц ресурса 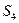. Так как потребление ресурсов 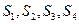не должно превышать запасов, соответственно 18, 16, 5 и 21 единицы, то связь между потреблением ресурсов и их запасами выразится системой неравенств:

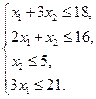(3)

По смыслу задачи переменные:

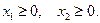(4)

Суммарная прибыль 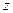составит 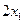руб. от реализации продукци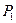и и 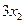руб. от реализации продукции 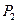, т.е.:

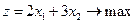(5)

Таким образом, получили экономико-математическую модель задачи: найти такой план выпуска продукции 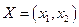, удовлетворяющий системе (3) и условию (4), при котором функция (5) принимает максимальное значение.

Задача составления рациона (задача о диете, задача о смесях).Имеются два вида корма I и II, содержащие питательные вещества (витамины) 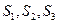. Содержание числа единиц питательных веществ в 1 кг каждого вида корма и необходимый минимум питательных веществ приведены в таблице 2:

Питательное Вещество (витамин)	Необходимый минимум питательных веществ	Число единиц питательных веществ в 1 кг корма
		I	II

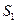
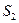
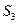
Стоимость 1 кг корма I и II соответственно равна 4 и 6 руб. Необходимо составить такой дневной рацион, имеющий минимальную стоимость,в котором содержание каждого вида питательных веществ было бы не меньше установленного предела.

Решение. Составим экономико-математическую модель задачи. Пусть 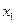и 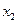- количество кормов I и II , соответственно, входящих в дневной рацион. Этот рацион будет включать 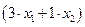единиц питательного вещества 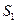; 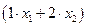единиц питательного вещества 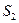; 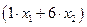единиц питательного вещества 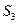. Так как содержание питательных веществ 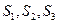, в рационе должно быть не менее, соответственно 9,8, 12 единицы, получим систему неравенств:

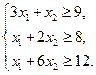(6)

По смыслу задачи переменные:

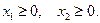(7)

Общая стоимость рациона z составит в руб.:

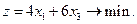(2)

Таким образом, получили экономико-математическую модель задачи: составить дневной рацион 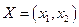, удовлетворяющий системе (6) и условию (7), при котором функция (2) принимает минимальное значение.