Постановка задачи линейного программирования
Пусть дана система т линейныхуравнений и неравенств с п переменными:
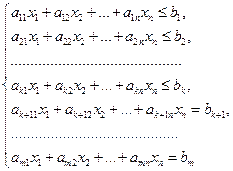 (1)
(1)
и линейная функция:
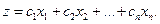 (2)
(2)
Требуется найти решение системы 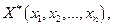
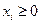
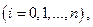 при котором функция z принимает оптимальное значение (максимальное или минимальное).
при котором функция z принимает оптимальное значение (максимальное или минимальное).
Такая задача называется задачей линейного программирования (ЗЛП) в общем виде. Система (1) называется системой ограничений; функция (2) называется целевой функцией (функцией цели).
Таким образом, задачи линейного программирования (ЛП) – это задачи, в которых линейны как целевая функция, так и ограничения в виде равенств или неравенств и для которых методы математического анализа оказываются непригодными. Задачи ЛП представляет собой наиболее часто используемый метод оптимизации.
К их числу относятся задачи:
- рациональное использование сырья и материалов; задачи оптимизации раскроя;
- рациональное использование сырья и материалов; задачи оптимизации раскроя;
- оптимизации производственной программы предприятий;
- оптимального размещения и концентрации производства;
- на составление оптимального плана перевозок, работы транспорта;
- управления производственными запасами
и многие другие, принадлежащие сфере оптимального планирования.
Около 75% от общего числа применяемых оптимизационных методов приходится на задачи ЛП. Около четверти машинного времени, затраченного в последние годы на проведение научных исследований, было отведено решению задач ЛП и их многочисленных модификаций.
ЗЛП можно записать в сокращенном виде:
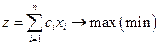 (
( 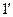 )
)
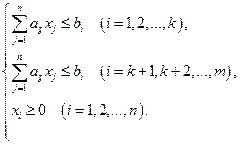 (
( 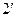 )
)
Оптимальным решением (планом) ЗЛП называется решение 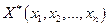 системы ограничений (2), при котором целевая функция принимает оптимальное значение.
системы ограничений (2), при котором целевая функция принимает оптимальное значение.
Если система ограничений (1) состоит из одних неравенств (не нарушая общности, будем говорить, что ограничения имеют вид « 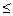 », так как, если знак неравенства «
», так как, если знак неравенства « 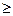 », то можно умножить его на -1 перейти к неравенству вида «
», то можно умножить его на -1 перейти к неравенству вида « 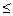 »), то такую задачу называют задачей линейного программирования в стандартном виде (в стандартной форме).
»), то такую задачу называют задачей линейного программирования в стандартном виде (в стандартной форме).
Если все ограничения системы (1) - уравнения (вида «=»), то такую задачу называют задачей линейного программирования в каноническом виде (в канонической форме).
Справедливо утверждение. Любая ЗЛП может быть приведена к каноническому виду.
Приведем ограничения (1) к каноническом виду:
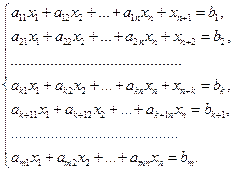
Теорема. Любому решению 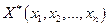 неравенства
неравенства 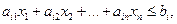
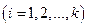 соответствует определенное решение
соответствует определенное решение 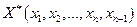 уравнения
уравнения 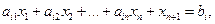 в котором
в котором 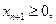 и наоборот.
и наоборот.
Дата добавления: 2017-04-05; просмотров: 2104;











