Переключательные функции. Существенные и несущественные переменные. Булевы функции одной переменной. Булевы функции двух переменных.
Функции вида f : E2n ® E2, где E2 = {0;1} – функции алгебры логики или булевы функции. Множество булевых функций от n переменных обозначим pn и
pn := { f | f : E2n ® E2}. Булеву функцию от n переменных можно задать таблицей истинности.
| x1 | … | xn–1 | xn | f(x1,…,xn) |
| … | ||||
| … | ||||
| … | ||||
| … | … | … | … | |
| … |
Если число переменных n, то в таблице истинности имеется 2n строк, соответствующих всем различным комбинациям значений переменных, которым можно сопоставить 22^n различных столбцов, соответствующих различным функциям. Т.о. число булевых функций от n переменных |pn| = 22^n. Булева функция f Î pn существенно зависит от переменной xi, если существует такой набор значений a1, a2,…, ai–1, ai+1,…, an–1, an, что выполняется условие f(a1, a2,…, ai–1, ai+1,…, an–1, an) ¹ f(a1, a2,…, ai–1, 1, ai+1,…, an–1, an). В этом случае xi – существенная переменная, в обратном случае xi – несуществующая (фиктивная) переменная.
Пример. Пусть булевы функции f1(x1, x2); f2(x1, x2) заданы следующей таблицей истинности:
| x1 | x2 | f1 | f2 |
Для этих функций переменная x1 – существенная, а x2 – несущественная. По определению булевы функции равны, если одна из другой получается введением (или удалением) несущественных переменных.
Функции называются эквивалентными, если их таблицы совпадают с точностью до переменных.
Для исключения фиктивной переменной удаляется столбец с этой переменной, дублирующие строки удаляются.
Булевы функции одной переменной представим в виде таблицы.
| Переменная x | f1(x) | f2(x) | f3(x) | f4(x) |
f1(x) – нулевая функция.
f1(x)=0
f2(x) – тождественная функция.
f2(x)=х
f3(x) – отрицание
–
f3(x) =х
f4(x) – единица.
f4(x)=1
Булевы функции двух переменных
| Обозначение функции | х1 | х2 | Наименование | ||
| Наборы | f= x1 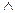 x2 x2
| ||||
| f1 | запрет x2 | ||||
| f2 | f= x1 | ||||
| f3 | запрет x1 | ||||
| f4 | тождественное x2 | ||||
| f5 | сложение по модулю 2 | ||||
| f6 | f= x1Úx2 (дизъюнкция) | ||||
| f7 | f= x1↓x2 (стрелка Пирса) | ||||
| f8 | f= x1~x2 (эквивалентность) | ||||
| f9 | f= | ||||
| f10 | f= x2→x1 | ||||
| f11 | f=(инверсия) | ||||
| f12 | f= x1→x2 | ||||
| f13 | f=x1|x2 | ||||
| f14 | f=1 |
В связи с ростом таблицы истинности используют их представления в виде формул. Обычно формула записывается в виде суперпозиции функций из базисного набора, который называют базисом.
Формулы. Реализация функций формулами. Равносильные формулы. Принцип двойственности.
Пусть F = {f1, f2,…,f2n} – множество булевых функций. Формулой над F называется выражение вида: f[F] = f(t1, t2,…,tn), fÎ F,ti – либо переменная, либо формула над F. Множество F – базис, функция f – главная (внешняя) функция (операция), ti – подформулы. Обычно для элементарных булевых функций используют инфиксную форму записи. Устанавливают следующий приоритет: Ø, &, Ú, ®. Ø отрицание или инверсия, & – конъюнкция, Ú дизъюнкция, ® импликация. Всякой формуле F однозначно соответствует функция f. Это соответствие задается алгоритмом интерпретации, который позволяет вычислить значение формулы при заданных значениях переменных. Зная таблицы истинности для функций базиса, можно вычислить таблицы истинности той функции, которую реализует данная формула.
Пример. Задана формула F1 := (x1 & x2) Ú ((x1 & ) Ú (& x2)).
Таблица истинности:
| x1 | x2 | x1 & | & x2 | (x1 & ) Ú ( & x2) | x1 & x2 | F1 |
Т.о. формула F1 реализует дизъюнкцию.
Одна функция может иметь множество реализаций над базисом. Формула, реализующая одну и ту же функцию, называется равносильной. Отношение равносильностей формул является эквивалентностью.
Имеют место следующие равносильности:
1. 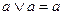
| 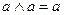
|
2. 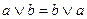
| 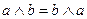
|
3. 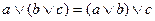
| 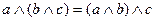
|
4. 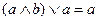
| 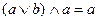
|
5. 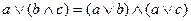
| 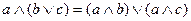
|
6. 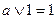
| 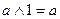
|
7. 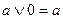
| 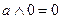
|
8. 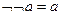
| |
9. 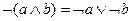
| 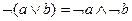
|
10. 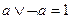
| 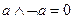
|
Принцип двойственности. Пусть f(x1,…,xn) Î Pn – булева функция. Тогда f*(x1,…,xn)(с чертой сверху) = f*(x1,…,xn)называется двойственной функцией f. f** = f.
Дата добавления: 2021-07-22; просмотров: 802;











