Конъюнктивная нормальная форма.

А называется элементарной дизъюнкцией, если она состоит из переменных и их отрицаний, связанных операцией дизъюнкции. Говорят, что А находится в КНФ, если она представляет собой конъюнкцию, возможно одночленную, элементарных дизъюнкций. КНФ: A = x₁ & ( Ú x₂) & (x₁ Ú ).

Теорема о приведении к КНФ. "A$B º A, находящаяся в КНФ. B называется КНФ А.

Доказательство:Аналогично теореме 1. Применяют обобщенные законы Де Моргана, чтобы привести операции отрицания к переменным. Применяют формулы дистрибутивности дизъюнкции относительно конъюнкции. A₃ º A и находится в КНФ.

Найдем КНФ для функций:

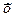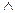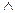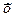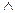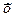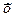f₁(х₁, х₂, х₃)= (х₁Úх₂Ú ₃ ) ( х₁ ÚÚ x₃ ) ( ₁Ú х₂Úx₃ ) ( ₁ÚÚ ₃ )

f₂(х₁, х₂, х₃)= (х₁Úх₂Ú x₃) 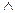( х₁ ÚÚ x₃ ) 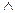( 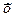₁Ú х₂Úx₃ ) 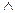( 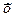₁ÚÚ x₃)

Тема 19. Неполностью определенные (частные) ПФ. Минимизация ПФ и неполностью определенных ПФ.