Минимальный каркас. Схема алгоритма построения минимальных каркасов.

<30 31 323334 35 36 >

Задача отыскания минимального каркаса (кратчайшего остова) – классическая задача теории графов. Методы решения этой задачи послужили основой многих других важных результатов (исследование алгоритма Краскала привели к созданию теории "жадных" алгоритмов).

Пусть G(V,E) – граф. Остов (каркас) – остовной подграф, являющийся деревом. Несвязный граф не имеет остова, связный граф может иметь много остовов. Если задать длины ребер, то можно поставить задачу нахождения кратчайшего остова, или минимального каркаса.

Пример: Пример практической интерпретации задачи нахождения кратчайшего остова. Пусть задано множество аэродромов, и нужно определить минимальный по сумме расстояний набор авиарейсов, который позволил бы перелетать с любого аэродрома на любой другой аэродром. Решение задачи – кратчайший остов полного графа расстояний между аэродромами.

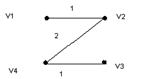
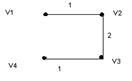
Граф расстояний между аэродромами и дерево кратчайших путей из вершины v1.

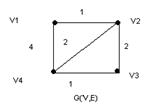
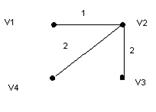
Кратчайшие остовы для графа G(V,E)

Рассмотрим схему алгоритма построения кратчайшего остова. Пусть Т – множество непересекающихся деревьев, являющихся подграфами графа G. Вначале Т состоит из отдельных вершин графа G, в конце Т содержит единственный элемент – кратчайший остов графа G.Схема алгоритма.

Вход: граф G(V,E), заданный матрицей длин ребер С.

Выход: кратчайший остов Т.

Т:=V

while в Т больше одного элемента do

взять любое поддерево из Т

найти к нему ближайшее

соединить эти деревья в Т

End while

Тема 17. Циклы и коциклы. Эйлеровы циклы. Гамильтоновы циклы. Теорема Дирака. Раскраска графов. Хроматическое число. Планарные графы. Укладка графов. Алгоритм раскрашивания.

<30 31 323334 35 36 >

Дата добавления: 2021-07-22; просмотров: 297;