Минимальные элементы. Теорема о существовании минимального элемента.

Теорема 3.2: Во всяком непустом конечном частично-упорядоченном множестве существует минимальный элемент.

Теорема 3.3:Всякий частичный порядок на конечном множестве может быть дополнен до линейного.

Вполне упорядоченное конечное множество содержит один минимальный элемент. А в произвольном конечном множестве их может быть несколько.

Замкнутость означает, что многократное выполнение заданных шагов не выходит за определенные границы

Определение 3.11. Пусть на множестве X задано отношение строгого порядка <. Элемент xÎX такой, что для всякого y из X, не совпадающего с x, выполнено соотношение x < y (x > y) называется наименьшим (наибольшим).

Определение 3.12. Пусть на множестве X задано отношение строго порядка <. Тогда элемент xÎX называется минимальным (максимальным) в упорядченом множестве
<X, < >, если не существует никакого элемента y, для которого y<x (соответственно y>x).

Если, как обычно, в случае x<y проводить стрелку от x к y, то в графе отношения минимальный элемент – это тот, в который не входят стрелки, а максимальный – из которого не выходят стрелки.

В случае линейного строго порядка минимальный элемент x обладает тем дополнительным свойством, что для всякого x¹y выполнено x<y. Тем самым для случая линейных порядков понятие минимального элемента совпадает с понятием наименьшего элемента. В общем случае может оказаться так, что элемент x минимален, но не находится в соотношении x<y с какими-то иными элементами. Например, на рисунке 3.4 элемент 2 является минимальным, но не сравним с элементами 3 и 7.

Чтобы понять различие между минимальным и наименьшим элементами, рассмотрим пример.

Пример. На рисунке 3.7 изображена диаграмма упорядоченного множества, в котором нет ни наименьшего, ни наибольшего элементов, но в то же время есть ровно 1 минимальный и ровно 1 максимальный элемент.

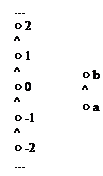
Рис.3.7. Упорядоченное множество

Рассмотрим подробнее конечные строго упорядоченные множества.

Лемма 3.1. Если на конечном (непустом) множестве X задан линейный строгий порядок, то существует наименьший элемент, и он единственен.

Доказательство. Возьмем произвольный элемент y₀ÎX. Если y₀- наименьший элемент, то существование искомого элемента доказано. Если нет, то поскольку < – линейный строгий порядок, существует такой элемент y₁¹ y₀, что y_1< y₀. Опять же либо y₁ – наименьший, либо существует y₂¹ y₁, такой, что y_2< y₁. Будем продолжать это процесс. Предположим, что уже выбрано n + 1 элементов, для которых y_n< y_n-1, y_n-1< y_n-2, …, y_1< y₀.

В силу транзитивности ясно, что y_i< y_j при i>j. Значит, в силу антирефлексивности, все выбранные элементы попарно не равны. Стало быть, ввиду конечности множества X процесс выбора должен прерваться за конечное число шагов. Элемент y_n, выбранный на последнем шаге, будет, очевидно, искомым. Итак, для любого z¹y_n выполнено y_n<z. Покажем, что этот элемент единственен. В самом деле, пусть существует другой элемент z¹y_n’ такой, что, для всякого z¹y_n, y_n’<z. Тогда одновременно выполняется y_n<y_n’ и y_n’<y_n, что невозможно в силу антисимметричности. Лемма доказана.

Теорема 3.4. Пусть дано отношение линейного строгого порядка < на конечном множестве X. Тогда на X можно выбрать такую нумерацию 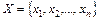, что соотношение 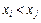будет выполняться в том и только в том случае, когда i<j.

Доказательство. Пусть x₁- наименьший элемент во множестве X, выбранный согласно лемме 1. Обозначим через X₁ множество 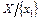. Обозначим через x₂ наименьший элемент множества X₁. Ясно, что x₁<x₂. Удалим из X₁ элемент x₂ и оставшееся множество обозначим через X₂. Его наименьший элемент x₃ удовлетворяет условию: x₂<x₃. Процедура нумерации уже ясна: перебирая по указанному методу последовательно все элементы из X, мы их выстроим в цепочку: 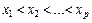, где p - количество элементов в X. В силу транзитивности и антисимметричности ясно, что x_i<x_j в том и только в том случае, когда i<j. Теорема доказана.

Эта теорема в сущности означает, что любой линейный строгий порядок на конечном множестве X равносилен обычному порядку на некотором отрезке натурального ряда.

С отношением порядка непосредственно связано отношение доминирования.

Определение 3.13. Пусть <X, α> - упорядоченное множество, x и y - его элементы. Будем говорить, что x доминирует над y, если 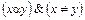, но не существует такого элемента zÎX, что .

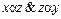С помощью отношения доминирования можно ввести другой наглядный способ изображения упорядоченных множеств - диаграммы Хассе. На диаграммах каждый элемент изображается точкой на плоскости, и если y доминирует над x, то точки x и y соединяют отрезком, причем точку, соответствующую x, располагают ниже y.

Рассмотрим три отношения частичного порядка и построим для них диаграммы Хассе.

Пример. Пусть A = {1, 2, 3}. На множестве всех подмножеств множества A рассмотрим отношение "быть подмножеством". Диаграмма этого упорядоченного множества приведена на рисунке 3.8(а).

Пример. Пусть X = {1, 2, 3, 5, 6, 10, 15, 30}. Введем на этом множестве отношение "делится". Диаграмма этого упорядоченного множества приведена на рисунке 3.8(б).

Пример. На множестве X = {1, 2, 3, 4, 5, 6, 7, 8} рассмотрим отношение линейного порядка <. Его диаграмма изображена на рисунке 3.8(в).

Рис. 3.8. Диаграммы Хассе

Заметим, что диаграммы Хассе первых двух отношений совпадают. Это означает, что эти частично упорядоченные множества имеют одинаковую структуру, причем отличную от структуры третьего упорядоченного множества, хотя оно тоже содержит восемь элементов. Более точно такая общность структуры определяется понятием изоморфизма (Тема 6).