Задачи оптимизации и задачи УО

Решение оптимизационной задачи может быть сведено к решению по­следовательности задач УО следующим образом. Находится допустимое ре­шение, после чего добавляется ограничение, соответствующее целевой функ­ции, которое выражает условие, что значение целевой функции должно быть лучше, чем для этого решения. Последовательные корректировки этого поро­гового значения, производимые до тех пор, пока задача не станет неразреши­мой, позволяют найти оптимальное решение.

Пример 10.1. Наиболее тривиальным алгебраическим примером задачи УО является задача решения системы уравнений. Дана система линейных уравнений над конечным полем 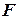. Имеет ли она решение? Ясно, что в этом примере каждое отдельное уравнение является ограничением, причем пере­менные уравнения образуют диапазон, а множество всех кортежей, соответ­ствующих решениям уравнения, образует отношение ограничения.

Пример 10.2. Задача стандартной пропозициональной 3-выполнимости (3-SAT) [4] определяется заданием формулы пропозициональной логики, состоящей из конъюнкции дизъюнктов, причем каждый дизъюнкт содержит 3 литерала (литерал ‑ это переменная или ее отрицание), и ответом на вопрос, имеются ли значения переменных, которые делают формулу истинной.

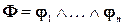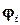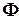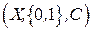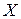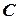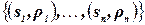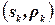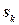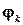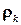Пусть ‑ такая формула, где ‑ дизъюнкты. Задача вы­полнимости для может быть выражена в виде задачи УО , где ‑ множество всех переменных в формуле, а ‑ множество ограничений , где каждое ограничение построено следующим обра­зом: ‑ список переменных, входящих в , а состоит из всех корте­жей, которые делают дизъюнкт 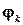истинным .

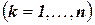Решения этой задачи УО ‑ присвоения значений переменным, которые делают формулу 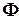истинной. Значит, любая задача 3-выполнимости может быть выражена в виде задачи УО.

Задача УО может быть также преобразована в задачу выполнимости SAT. Для данной ЗУО 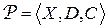построим задачу выполнимости SAT сле­дующим образом. Введем 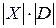переменных 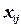. Переменные 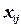принимают значение «истина» тогда и только тогда, когда переменной 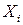присвоено значе­ние 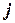. Для каждой переменной добавляются клаузы (дизъюнкты) 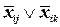для всех пар значений одной и той же переменной, чтобы гарантиро­вать невозможность одновременного принятия переменной двух различных значений. Добавляется дизъюнкт 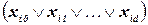, чтобы гарантировать, что переменной присвоено хотя бы одно значение.

Пример 10.3. Любая конкретная задача УО может быть выражена в логи­ческой форме.

Действительно, используя стандартное соответствие между отноше­ниями и предикатами, можно переписать задачу УО в виде формулы первого порядка 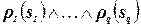, где 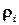‑ предикаты на 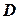и 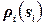означает преди­кат 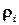, примененный к кортежу 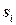переменных .

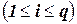Вопрос состоит в том, является ли эта формула выполнимой. Эта задача обычно используется в теории баз данных, поскольку она соответствует оценке конъюнктивного запроса, как показано в следующем примере.

Пример 10.4. Реляционная база данных может быть рассмотрена как ко­нечное множество таблиц. Таблица состоит из схемы и конкретных данных, где схема ‑ конечное множество атрибутов, причем каждый атрибут имеет соответствующее ему множество возможных значений, называемое доменом. Конкретные данные ‑ это конечное множество строк, где каждая строка ‑ ото­бражение, ставящее в соответствие каждому атрибуту схемы значение из ее домена.

Стандартной задачей для реляционных баз данных является задача оценки конъюнктивного запроса, в которой спрашивается, имеет ли решение конъюнктивный запрос, т.е. запрос вида 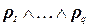, где 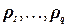‑ атомарные формулы. Конъюнктивный запрос над реляционной базой данных соответст­вует конкретному примеру задачи УО, что достигается простой заменой тер­минов: «атрибуты» заменяются на «переменные», «таблицы» ‑ на «ограниче­ния», «схема» ‑ на «диапазон», «конкретные данные» ‑ на «отношение огра­ничения», а «строки» ‑ на «кортежи». Значит, конъюнктивный запрос эквива­лентен конкретному примеру задачи УО, переменные которой – это атрибуты запроса. Для каждой атомарной формулы 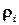в запросе найдется ограничение 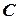такое, что диапазон ограничения 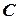‑ это список переменных формулы 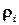и отношение ограничения 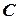‑ это множество моделей .

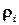Пример 10.5. Интервальные задачи УО.

Одним из видом задач УО с доменами, содержащими бесконечное число значений, являются задачи УО, в которых значения, принимаемые пе­ременными, являются интервалами действительной прямой. Эти задачи ис­пользуются для моделирования поведения во времени систем, где интервалы представляют интервалы времени, в течение которых происходят события.

Наиболее популярной формальной структурой такого рода является интервальная алгебра Аллена (ИАА)[3], описывающая бинарные качественные отношения между интервалами.

ИАА содержит 13 базовых отношений, соответствующих 13 различным способам, согласно которым могут соотноситься два интервала. Полная сис­тема отношений в ИАА состоит из 2¹³ = 8192 возможных объединений базо­вых отношений.

Интервальная алгебра Аллена имеет три операции над отношениями: композиция, пересечение и инверсия.