Определение задачи удовлетворения ограничений

Использование подходов и алгоритмов искусственного интеллекта (ИИ) позволяет решать многие прикладные задачи, такие, как задачи теории распи­саний, задачи проектирования экспертных систем и систем поддержки приня­тия решений[1], доказательство теорем, задачи тестирования элек­тронных схем, обработка изображений.

Одной из важных задач ИИ является задача удовлетворения ограниче­ний (УО) (constraint satisfaction problem). Теория УО предлагает удобный аппарат и простую формальную схему для представления и решения комбинаторных задач ИИ. Целью решения задачи УО является нахождение значений переменных, удовлетворяющих заданным ограничениям.

Парадигма УО является обобщением пропозициональной логики, в ко­торой переменным могут быть присвоены значения из множества любого числа переменных, а не только «истина» и «ложь».

Проблема существования решений задачи УО является NP-полной.

В искусственном интеллекте парадигма УО признана в качестве удоб­ного и эффективного способа моделирования и решения многих прикладных задач, таких как планирование и календарное планирование, задачи назначе­ния радиочастот, обработка изображений, тестирование сверхбольших интегральных схем СБИС (VLSI), анализ языков программирования и пони­мание естественного языка. В теории баз данных показано, что ключевая за­дача оценки конъюнктивных запросов может рассматриваться как задача УО.

Программирование в ограничениях является парадигмой программиро­вания для декларативного описания и эффективного решения комбинаторных задач, тесно связанной с теорией УО.

Многие классические комбинаторные задачи, такие как известная тео­рема Ферма, задача выполнимости (SAT) из пропозициональной логики, за­дача раскраски графа и задача изоморфизма графов из теории графов могут формулироваться в виде за­дач УО (ЗУО).

Остановимся подробнее на одной из давно поставленных задач в мате­матике ‑ задаче о раскраске графа (раскраска карты ‑ частный случай этой за­дачи, описанной в разделе 4.2.1). Формулировка задачи о раскраске в виде задачи УО ставит в соответст­вие вершинам раскрашиваемого графа переменные, возможные цвета пред­ставляют собой домены (области определения) переменных, а ограничения-неравенства между смежными вершинами являются ограничениями задачи.

Разумеется, в рамках данных обзорных лекций невозможно под­робно описать все аспекты и направления теории удовлетворения ограниче­ний и программирования в ограничениях, поэтому более полную информа­цию можно найти в монографии [33], а также в переводной монографии [26].

Цель настоящей главы ‑ дать представление об основных направле­ниях теории УО и программирования в ограничениях.

Коснемся вначале терминологии и истории возникновения методов УО.

Montanari[2] предложил использовать модели УО для опи­сания ряда комбинаторных задач, возникающих при компьютерной обработке изображений, и назвал эти задачи УО «сетями ограничений» (networks of constraints). Это связано с тем, что систему ограничений можно представить в виде неориентированного графа с вершинами-переменными и ребрами, соот­ветствующими ограничениям между двумя переменными. По мнению Dechter [33], сети ограничений являются графовым представлением, используемым для поиска стратегий решения задач УО.

Достаточно быстро этот подход был использован для решения гораздо более широкого класса задач. В научной литературе используются оба этих термина ‑ сети ограничений и задачи удовлетворения ограничений.

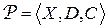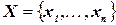Задача удовлетворения ограничений (УО) представляет собой кортеж , где ‑ множество переменных, 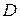‑ множество доменов значений переменных, 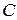‑ множество ограничений.