МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ И АСПЕКТЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ СЛОЖНЫХ ТЕХНИЧЕСКИХ СИСТЕМ

3.1. Автоматизация функционального проектирования.
Задачи функционального проектирования

Функциональное проектирование включает в себя решение трудоемких задач, связанных с определением принципов построения объектов проектирования и оценкой их свойств на основе исследования процессов их функционирования. Автоматизация функционального проектирования предполагает решение этих задач с помощью функциональных математических модулей (ММ) объектов проектирования на микро-, макро-, и метауровнях.

Основой функционального проектирования является одновариантный анализ объектов проектирования – определение выходных параметров объекта при заданных значениях внутренних и внешних параметров. Большинство задач одновариантного анализа (моделирование переходных процессов, статических режимов, частотных характеристик и др.) сводится к решению систем обыкновенных дифференцированных уравнений (ОДУ), а также систем нелинейных и линейных алгебраических уравнений (АУ). В связи с этим эффективность автоматизации функционального проектирования будет в значительной степени определяться эффективностью методов и алгоритмов для численного решения этих систем.

Успешное решение задач одновариантного анализа создает предпосылки для постановки и решения задач многовариантного анализа, т. е. исследования поведения объекта проектирования при изменении его внутренних и внешних параметров.

Важнейшей задачей функционального проектирования является поиск оптимальных значений внутренних параметров объекта при заданном техническом задании. Эту задачу призвана решать параметрическая оптимизация, объединяющая два важных аспекта: постановки задачи и выбора методов ее решения. Среди задач функционального проектирования определение структуры объекта (структурный синтез) наименее формализовано.

3.2. Одновариантный анализ

Основным видом одновариантного анализа объектов проектирования является анализ переходных процессов, при котором определяются зависимости фазовых переменных (выходных параметров) от времени при заданных значениях внутренних и внешних параметров. Фазовые переменные характеризуют физическое или информационное состояние объекта.

Математическая модель (ММ), описывающая динамические свойства объектов, представляет собой систему обыкновенных дифференциальных уравнений (ОДУ). При этом ММ может быть получена либо в нормальной форме Коши, либо в неявной форме ОДУ.

Нормальная форма Коши

dU / dt = F (U, t), (1)

где U – вектор переменных состояния моделируемого объекта размерностью n, т.е. вектор тех фазовых переменных, которые характеризуют запасы энергии в физической системе либо ее информационное состояние; F – вектор-функция, t – время (начальные условия U = U₀ | t=0).

Неявная форма ОДУ

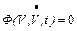(2)

где V – вектор фазовых переменных, достаточных для определения состояния моделируемого объекта, размерностью n; 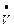= dV / dt – вектор производных фазовых переменных по времени, причем вектор 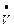имеет только l ненулевых элементов (l ≤ n); Ф – вектор-функция (начальные условия V = V₀ | t=0).

Система (1) является частным случаем системы (2), если последнюю удается разрешить относительно вектора V.

Анализ переходных процессов сводится к численному интегрированию (1) или (2). Представление системы ОДУ в виде (1) наиболее удобно для решения ОДУ на ЭВМ. Интегрирование системы (1) заключается в определении значений U(t) на интервале времени 0…T_кон при заданных начальных условиях U₀. При решении этой задачи на интервале интегрирования выделяются конечное число точек t_m, в которых определяются значения U. Интервал между соседними точками называется шагом интегрирования и обозначается h_m = (t_m+1 - t_m).

Для большинства проектируемых динамических объектов переходные процессы носят асимтотически устойчивый характер, т.е. при t → ∞ объект переходит в определенное устойчивое состояние. В связи с этим важной задачей одновариантного анализа в САПР является расчет значений фазовых переменных объекта в устойчивом состоянии или расчет статического режима объекта. Иногда динамический объект имеет несколько устойчивых состояний, тогда необходимо рассчитать несколько его статических режимов.

Статический режим можно рассчитать, интегрируя исходную систему ОДУ на достаточно большом интервале времени. Этот метод называется методом установления. Он надежен но не всегда эффективен, так как требует значительных затрат машинного времени. В статическом режиме производные фазовых переменных по времени равны нулю и отсутствуют меняющиеся во времени внешние воздействия, поэтому ММ статических состояний можно определить непосредственно из ММ динамических процессов (1) или (2). В результате получим системы алгебраических уравнений относительно соответствующих переменных

F (U) = 0 или Ф (V) = 0.

Таким образом, одновариантный анализ статических режимов физических объектов, описываемых системой ОДУ, сводится к решению системы АУ n-го порядка общего вида

F (x) = 0,

где x – вектор неизвестных размерностью n.

Для решения АУ применяют итерационные методы. Основные характеристики итерационных методов решение систем АУ – сходимость итераций и скорость сходимости к точному решению, определяющие алгоритмическую надежность, точность и экономичность для этих методов.

3.3. Многовариантный анализ

Одновариантный анализ является необходимой составной частью более сложных задач многовариантного анализа, оптимизации и структурного синтеза. В этих случаях задачи одновариантного анализа – необходимая предпосылка для успешного выполнения многовариантного анализа и оптимизации сложных технических объектов. Можно выделить два направления повышения эффективности одновариантного анализа: 1) разработка специальных методов и алгоритмов, рассчитанных на ограниченный класс объектов проектирования; 2) разработка универсальных методов и алгоритмов, пригодных для большинства проектируемых объектов.

Специальные алгоритмы позволяют достигнуть максимальной эффективности одновариантного анализа, так как дают возможность наиболее полно учитывать специфические особенности конкретных объектов. Однако область применения таких алгоритмов ограниченна.

Универсальные методы анализа повышенной эффективности учитывают особенности ММ, присущие большинству объектов проектирования (высокую размерность решаемых проектных задач, разреженность матриц в ММ, жесткость систем ОДУ, умеренные требования к точности анализа). К универсальным методам анализа повышенной эффективности можно отнести: комбинированные методы (алгоритмы) интегрирования систем ОДУ; методы разреженных матриц; диакоптические и адаптивные методы анализа.

Основная особенность комбинированных алгоритмов – автоматическая адаптация используемых базовых методов численного интегрирования ОДУ в ходе решения задачи с целью получения точных и надежных результатов при максимальной экономии вычислительных ресурсов. Базовые методы численного интегрирования ОДУ делятся на явные и неявные (Эйлера, Рунге-Кута, Адамса). Явные методы требуют меньших вычислительных затрат на шаг интегрирования, но имеют ограниченную область устойчивости и неэффективны при решении ОДУ с большим разбросом постоянных времени. Неявные методы более универсальны, но на каждом шаге интегрирования требуют решения систем АУ. Комбинированные алгоритмы интегрирования позволяют совместить достоинства явных и неявных методов.

Разряженная матрица – матрица, имеющая большое число нулевых элементов. Основная идея методов разряженных матриц состоит в том, чтобы в ходе решения системы хранить только ненулевые элементы матрицы и вычисления производить только с ними.

Диакоптические методы анализа (методы разбиения, декомпозиции) основаны на разделении сложной системы уравнений высокой размерности на более простые подсистемы с учетом связей между ними. В результате решения задача высокой размерности сводится к последовательному (возможно, и параллельному) решению нескольких задач меньшей размерности. Каждая подсистема, в свою очередь, может разбиваться на более простые подсистемы. Разбиению системы уравнений на подсистемы соответствует разбиение исследуемого объекта на части, что обычно осуществляет инженер-проектировщик, учитывающий при этом функциональную законченность частей и их повторяемость в структуре объекта.

Отличительная особенность диакоптических методов анализа – возможность организации независимых вычислительных процессов отдельно для каждой подсистемы уравнений. Но для получения достоверных результатов нужно учитывать взаимовлияние подсистем. Поэтому в диакоптических методах периодически проводятся согласование результатов вычислений в независимых подсистемах.

Сущность адаптивных методов анализа заключается в следующем. При анализе сложных объектов на каждом этапе вычислительного процесса можно выбрать наиболее эффективную модель объекта и наиболее эффективные алгоритмы анализа с точки зрения минимизации вычислительных затрат и обеспечения необходимой точности расчета. Автоматизация смены моделей и алгоритмов при расчете составляет основу адаптивных методов анализа. В этих методах предполагается, что ММ объекта может содержать модели элементов на всех уровнях моделирования (микро-, макро- и метауровне). В результате возникают две основные проблемы: 1) выбор алгоритмов анализа на разных уровнях моделирования, отвечающих требованиям смешанного анализа, и синхронизация вычислительных процессов при проведении совместного расчета по этим алгоритмам; 2) разработка моделей элементов – преобразователей фазовых и информационных переменных для организации связей между разноуровневыми моделями.