Процедуры параметрической оптимизации

Поиск рационального технического решения при выбранном физическом принципе действия осуществляется методами структурного синтеза. Определение оптимальных значений параметров элементов технической системы известной структуры – задача параметрического синтеза или параметрической оптимизации.

Постановка задачи оптимизации имеет содержательный смысл только в том случае, когда появляется необходимость выбора одного из конкурирующих вариантов, полученных при ограниченности ресурсов. Техническое проектирование всегда ведется в условиях жестких ограничений на материальные, энергетические, временные и прочие виды ресурсов. Вместе с тем средства САПР позволяют выполнить разработку большого количества альтернативных вариантов. Поэтому окончательный выбор технического объекта (принятие решения) необходимо проводить с учетом выработанных правил предпочтения на основании установленных критериев. Выбор критерия является одним из важных этапов постановки задачи оптимизации, так как все последующие действия направлены на поиск объекта, наиболее близкого к оптимальному по выбранному критерию.

В основе построения правила предпочтения лежит целевая функция, количественно выражающая качество объекта и потому называемая также функцией качества или критерием оптимальности.

Проблема оптимизации имеет два основных аспекта: 1) необходимо поставить задачу, формализовав понятие «оптимальный»; 2) необходимо решить задачу, уже имеющую математическую формулировку. Процедура постановки задачи носит неформальный характер и включает следующие этапы: выбор целевой функции и управляемых параметров; назначение ограничений; нормирование управляемых и выходных параметров и т.п.

Сложность выбора целевой функции состоит в том, что любой технический объект первоначально имеет векторный характер критериев оптимальности (многокритериальность). Улучшение одного из выходных параметров, как правило, приводит к ухудшению другого, так как все выходные параметры являются функциями одних и тех же управляемых параметров и не могут изменяться независимо друг от друга. Такие выходные параметры называют конфликтными параметрами. Целевая функция должна быть одна (принцип однозначности). Сведения многокритериальной задачи к однокритериальной называют сверткой векторного критерия. Задача поиска его экстремума сводится к задаче математического программирования.

3.5. Имитационное моделирование в функциональном
проектировании. Понятия имитационного моделирования

Сложность и многообразие процессов функционирования исследуемых технических систем не всегда позволяют получать для них адекватные математические модели, сформулированные в виде различных аналитических соотношений. Автоматизированное проектирование, анализ и оценка функционирования систем в этих случаях базируется на использовании методологии имитационного моделирования.

Имитационное моделирование – метод исследования, основанный на том, что изучаемая динамическая система заменяется ее имитатором и с ним проводятся эксперименты на ЭВМ с целью получения информации об изучаемой системе. Ключевым моментом при этом является выделение и описание состояний системы. Система характеризуется набором переменных, каждая комбинация значений которых описывает ее конкретное состояние. Следовательно, путем изменения значений переменных можно имитировать переход системы из одного состояние в другое. Таким образом, имитационное моделирование – это представление динамического поведения системы посредством продвижения ее от одного состояния к другому в соответствии с хорошо определенными операционными правилами. Изменения состояния системы могут происходить либо непрерывно, либо в дискретные моменты времени.

При построении имитационной модели (ИМ) предусматривают прежде всего возможность вычисления некоторого функционала, заданного на множестве реализаций процесса функционирования изучаемой системы и характеризующего поведение объекта имитации. Наиболее важным функционалом для технической системы является показатель ее эффективности. Имитируя различные реальные ситуации на имитационной модели, получают возможность решения таких задач, как оценка эффективности различных принципов управления системой, сравнение вариантов структуры системы, определение степени влияния изменений параметров системы и начальных условий имитации ее поведения на показатель эффективности.

Таким образом, имитация предназначена для построения идеализированного процесса функционирования системы, называемого имитационным процессом. Процесс функционирования реальной системы распадается на ряд процессов функционирования отдельных объектов. Эти процессы протекают одновременно, или параллельно. Задача программной имитации состоит в отображении параллельно протекающих процессов на один вычислительный процесс.

Множество моментов времени изменения состояния системы конечно и может быть описано выражением

T = <t₁, t₂…, t_i,…, t_n >,

где t_i – i-й момент времени изменения состояния системы; t_n – общее время наблюдения за системой. Каждому моменту времени t_i соответствует оператор Н_i, вычисляющий состояние S_i , где s_i Î S. Оператор Н_i, осуществляет отображение времени t_i на один из элементов множества пространства состояний системы S.

Предположим, что выполнение оператора Н_i происходит мгновенно в момент времени t_i . В общем случае оператор Н_i можно представить в следующем виде:

s = H (A, t, ω),

где s Î S – состояние процесса Z; А – пространство аргументов; t – текущее значение времени; ω – случайная величина, распределенная равномерно на отрезке [0, 1], принимающая новое значение при каждом выполнении оператора Н. Использование величины ω позволяет описать случайность в операторе. Таким образом, для момента времени t_i

s_i = H_i (A_i, t_i, ω).

Если для двух произвольных моментов времени t_i и t_j оказывается s_iÎA_j , то будем называть операторы H_i и H_j сцепленными и обозначать H_i≈ H_j. Практически это обозначает, что для вычисления состояния s_j в момент времени t_j необходимо знать состояние s_i в момент времени t_i. Под функционированием системы понимается процесс изменения ее состояния во времени. Этот процесс назовем процессом функционирования

S = <T, S, F, α>,

где S – пространство состояний; F – траектория процесса (F:T 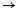S); α – отношение линейного порядка на множестве моментов времени T.

В зависимости от типа процесса множество моментов времени T может быть как непрерывным, так и дискретным. Если T заданно в виде упорядоченных чисел, то величину α из данного выражения можно исключить. Пространство состояний S определяется параметрами системы. Пусть W – множество параметров системы. Под параметром Р системы будем понимать некоторую скалярную переменную, обладающую именем и множеством значений:

Р = <W_P, σ (W_P) >,

где W_P – имя параметра; σ (W_P) – множество значений параметра, элементы множества σ (W_P) скалярны.

При этих условиях пространство состояний

S =П σ (w) для всех w Î W,

где П – символ декартова произведения множеств.

Таким образом, размерность пространства S равна числу параметров системы.

Программная имитационная модель реализуется на ЭВМ в виде последовательного вычислительного процесса. Выполнение элементарного оператора называется событием. При реализации программы имитационной модели параллельные процессы функционирования моделируемой системы отображаются на один последовательный процесс вычислений, реализуемый ЭВМ. Главные задачи при осуществлении такого отображения – продвижение модельного времени и формирование для каждого момента времени класса одновременных событий (КОС). Первое событие в КОС – активное. Признак окончания КОС – нулевые значения всех условий в элементарных операторах.