Изменение скорости жидкости в поперечном сечении трубы

(поперечное поле скоростей)

В случае плавного входа жидкости в трубу можно считать, что поле скоростей во входном сечении трубы равномерное. При течении жидкости в трубе на некоторой ее длине происходит изменение формы (деформация) поперечного поля скорости - за счет трения скорость жидкости у стенки уменьшается, а в области оси увеличивается, так как расход жидкости вдоль трубы остается постоянным. Участок трубы, на котором происходит деформация поля скорости, называется участком гидродинамической стабилизации течения или начальным участком. В конце этого участка формируется течение с поперечным полем скорости, которое остается неизменным при дальнейшем течении жидкости в трубе. Такое течение называется автомодельным, а участок трубы с автомодельным течением - основным. Формулу для расчета скорости в поперечном сечении автомодельного течения жидкости в трубе можно получить двумя путями: из уравнения количества движения для элементарной струйки и, используя систему дифференциальных уравнений, описывающих течение жидкости в трубе. Второй вариант приводится в 1.1.5.1.

Получим формулу для расчета скорости в поперечном сечении автомодельного ламинарного течения жидкости в трубе из уравнения количества движения элементарной струйки.

При осесимметричном ламинарном течении жидкости в круглой трубе касательное напряжение, действующее вдоль поверхностей соприкосновения слоев жидкости, пропорционально поперечному градиенту скорости:

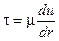. (1.1)

В этой формуле: t - касательное напряжение, u – скорость жидкости, направленная параллельно оси трубы, r - ось координат, направленная вдоль радиуса трубы (по нормали к оси трубы).

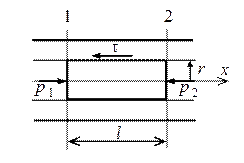Выделим в трубе цилиндрическую элементарную струйку радиусом r, ось которой совпадает с осью трубы (рис. 1.2). Запишем для сечений 1 и 2 этой струйки уравнения неразрывности и количества движения

r₁u₁F₁ = r₂u₂F₂

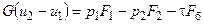
В этих уравнениях: r и u - плотность и скорость жидкости в элементарной струйке, F - площадь поперечного сечения струйки (F = pr²), G - расход жидкости через поперечное сечение струйки, р - давление, t - напряжение трения, F_б - площадь боковой поверхности элементарной струйки (трубки тока) между сечениями 1 и 2 (F_б = 2prl). Уравнение количества движения записано в предположении отсутствия объемных сил.

Так как r₁ = r₂ и F₁ = F₂, то из уравнения неразрывности следует, что u₁ = u₂. С учетом этого из уравнения количества движения получаем

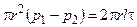
Замена в этом уравнении t с использованием (1.1) дает

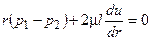
В результате интегрирования последнего уравнения получается уравнение для скорости в точке, расположенной на расстоянии r от оси трубы

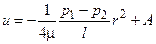(1.2)

Здесь А - постоянная интегрирования, которая находится из граничного условия: u = 0 при r = R:

.

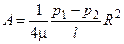Подставляя значение А в (1.2), получаем:

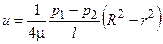(1.3)

В последней формуле: (р₁ - р₂) = Dр - изменение давления жидкости в трубе на длине l, R - радиус трубы, r - текущий радиус.

Максимальное значение скорости жидкости соответствует оси трубы при r = 0

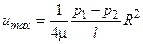(1.4)