Системы единиц физических величин

ИЗМЕРЕНИЕ ФИЗИЧЕСКИХ ВЕЛИЧИН

Для более детального изучения физических величин их классифицируют на группы (рис. 1.1). По принадлежности к различным группам физических явлений физические величины делятся на пространственно-временные, механические, тепловые, электрические и магнитные, акустические, световые, физико-химические и др.

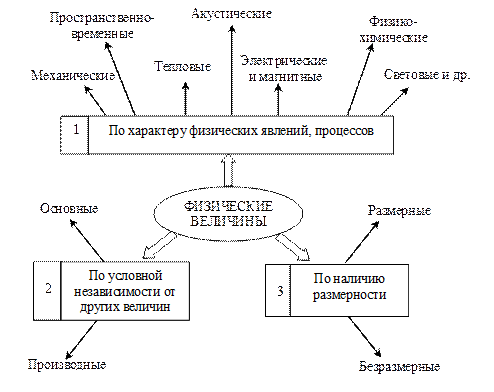
Рис. 1.1. Классификация физических величин

По степени условной независимости от других величин физические величины подразделяют на основные и производные. В настоящее время в Международной системе единиц используют семь величин, выбранных в качестве основных (независимых одна от другой): длина, время, масса, температура, сила электрического тока, количество вещества и сила света. Остальные величины, такие как плотность, сила, энергия, мощность и др. являются производными (т.е. зависимыми от других величин).

По наличию размерности физические величины делят на размерные, т.е. имеющие размерность и безразмерные.

Размер физической величины характеризует количественное содержание свойства в каждом объекте. Значение физической величины – это выражение ее размера в виде некоторого числа принятых для нее единиц измерения. Например, 0,001км; 1 м; 100 см; 1000мм – 4 варианта представления одного и того же размера длины.

Числовое значение физической величины – это число, выражающее отношение значения величины к соответствующей единице измерения.

Единица измерения представляет собой величину фиксированного размера, которой условно присвоено числовое значение, равное 1, и применяемое для количественного выражения однородных с ней физических величин.

В настоящее время установлено следующее определение измерения:

Измерение есть совокупность операций по применению технического средства, хранящего единицу физической величины, обеспечивающих нахождение соотношения измеряемой величины с ее единицей и получения значения этой величины.

Итак, если имеется некоторая величина Q, принятая для нее единица измерения, равная [Q], то размер физической величины

Q = q×[Q], (*)

где q – числовое значение величины Q.

Выражение q×[Q] – есть результат измерения, оно составлено из двух частей: числового значения q, которое является отношением измеряемой величины к единице измерения (оно может быть целым или дробным), и единицы измерения [Q]. Обычно единицу физической величины хранит используемое для измерения техническое устройство – средство измерения.

Допустим, при измерении длины детали получен результат измерения 101,6 мм. В этом случае за единицу длины принят [1 мм], числовое значение q = 101,6. Если же за единицу принять [1 см], то q = 10,16.

Уравнение (*) называют основным уравнением измерений, т.к. оно описывает измерение как процесс сравнения физической величины с её единицей измерения.

Для измерения величины могут быть выбраны различные единицы, т.е.

Q = q₁×[Q]₁ = q₂×[Q]₂

Из этого выражения следует, что числовое значение величины обратно пропорционально размеру единицы: чем больше размер единицы, тем меньше числовое значение величины, и наоборот:

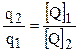
Кроме того, уравнение показывает, что размер физической величины Q не зависит от выбора единицы измерения.

Таким образом, числовые значения измеряемых величин зависят от того, какие используются единицы измерения. Выбор единиц имеет большое значение для обеспечения сравнимости результатов измерений; допустить произвол в выборе единиц – значить нарушить единство измерений. Именно поэтому в большинстве стран мира размеры единиц измерений закреплены законодательно (т.е. узаконены). В России в соответствии с Законом «Об обеспечении единства измерений» допускаются к применению единицы Международной системы единиц.

Измерение значимо лишь тогда, когда по его результату можно оценить истинное значение величины. При анализе измерений следует четко различать эти два понятия: истинное значение физической величины и его эмпирическое проявление – результат измерения.

Любой результат измерений содержит погрешность вследствие несовершенства средств и методов измерений, влияния внешних условий и других причин. Истинное значение измеряемой величины остается неизвестным. Его можно представить только теоретически. Результат измерения величины лишь в большей или меньшей степени приближается к ее истинному значению, т.е. представляет его оценку.

Шкалы измерений

Шкала измерения служит исходной основой для измерений данной величины. Она представляет собой упорядоченную совокупность значений величины.

Практическая деятельность привела к формированию различных видов шкал измерений физических величин, основными из которых являются четыре:

1. Шкала порядка (рангов) представляет собой ранжированный ряд – упорядоченную по возрастанию или убыванию последовательность величин, характеризующих изучаемое свойство.

2. Шкала интервалов (разностей) отличается от шкалы порядка тем, что для измеряемых величин вводятся не только отношения порядка, но и суммирования интервалов (разностей) между различными количественными проявлениями свойств.

Шкалы интервалов являются более совершенными, чем шкалы порядка. В этих шкалах над величинами можно проводить аддитивные математические операции (сложение и вычитание), но нельзя – мультипликативные (умножение и деление).

3. Шкала отношений описывает свойства величин, для которых применимы отношения порядка, суммирования интервалов и пропорциональности. В этих шкалах существует естественный нуль и по согласованию устнавливают единицу измерения. Шкала отношений служит для представления результатов измерений, полученных в соответствии с основным уравнением измерений путем экспериментального сравнения неизвестной величины Q с ее единицей [Q]. Примерами шкал отношений являются шкалы массы, длины, скорости, термодинамической температуры.На шкале отношенийопределены любые математические операции.

4. Абсолютная шкала обладает всеми признаками шкалы отношений, но дополнительно в ней существует естественное однозначное определение единицы измерений. Такие шкалы используют для измерений относительных величин (коэффициенты усиления, ослабления, полезного действия, отражения, поглощения.

Шкалы интервалов и отношений объединяют термином «метрические шкалы». Шкалу порядка относят к условным шкалам, т.е. к шкалам, в которых не определена единица измерения и иногда называют неметрической. Абсолютные и метрические шкалы относят к разряду линейных. Практическая реализация шкал измерений осуществляется путем стандартизации как самих шкал и единиц измерений, так и, в необходимых случаях, способов и условий их однозначного воспроизведения.

Системы единиц физических величин

Наличие ряда систем единиц физических величин, значительного числа внесистемных единиц, а также неудобства, связанные с пересчетом при переходе от одной системы единиц к другой, потребовало унификации единиц измерений. Рост научно-технических и экономических связей между разными странами обусловливал необходимость такой унификации в международном масштабе.

Требовалась единая универсальная система единиц величин, практически удобная и охватывающая различные области измерений, которая могла бы стать международной. При этом она должна обладать когерентностью (равенством единице коэффициента пропорциональности в уравнениях связи между физическими величинами).

В 1960 г. XI Генеральная конференция по мерам и весам утвердила Международную систему единиц, обозначаемую сокращенно SI (начальные буквы французского наименования Systeme International d¢Unites), в русской транскрипции – СИ.

<12 3 4 5 6 7 >

Дата добавления: 2017-03-12; просмотров: 2005;