Нормальный закон распределения случайной величины. Параметры нормального распределения

Математическое описание непрерывных случайных величин (к числу которых относится и 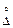), осуществляется обычно с помощью законов распределения случайной величины. Эти законы определяют связь между возможным значением случайной величины и соответствующей ему плотности вероятности.

Наиболее распространенным при измерениях является нормальный закон распределения (рис. 1.9). Он наблюдается, когда расхождения результатов обусловлены большим числом независимых причин и ни одна из них не доминирует над остальными. На рис. 1.10, а показана кривая нормального распределения для некоторой измеряемой величины Х. По оси абсцисс отложены значения величины Х, а по оси ординат – вероятность их появления р(Х). Кривая нормального распределения симметрична линии, проходящей через центр распределения M[Х] (математическое ожидание), и имеет колоколообразную форму. Рассеяние результатов отдельных измерений относительно центра распределения характеризуется средним квадратическим отклонением s. Математическое ожидание M[Х] является тем значением величины, вокруг которого группируются результаты отдельных измерений. s является мерой рассеяния результатов относительно M[Х], т.е. характеризует форму кривой распределения.

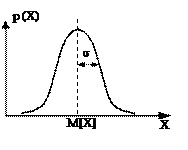
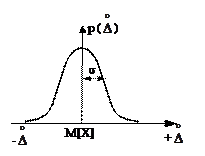
а	б

Рис. 1.10. Кривые нормального распределения: а – случайной величины Х, б – случайной погрешности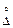

Перенеся начало координат в точку M[Х], получим кривую распределения случайной погрешности (рис. 1.10, б).

На рис. 1.11 приведены кривые нормального распределения при различных значениях s (рассеяния результатов). Сравнивая их между собой, можно установить, что рассеяние для кривой 2 меньше, чем для кривой 3, но больше, чем для кривой 1. Очевидно, что наиболее высокая сходимость наблюдается для результатов измерений, распределенных в соответствии с кривой 1.

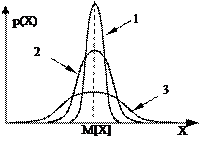
Рис. 1.11. Кривые нормального распределения с разным рассеянием значения величины, s₁ < s₂ < s₃

Математическое выражение для описания кривой нормального распределения случайной величины (рис. 1.10, а), предложенное Гауссом, имеет вид

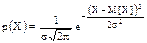
Для описания кривой нормального распределения случайной погрешности (рис. 1.10, б) это выражение можно переписать в виде

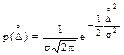
M[Х] и s являются двумя важнейшими параметрами нормального распределения случайной величины. Достаточно знать эти параметры, чтобы задать нормальное распределение.

Правило трех сигм

Характерное свойство нормального распределения состоит в том, что в интервале [M[Х] ± 1s] находится около 68 % из всех его результатов измерений. В интервале [M[Х] ± 2s] - 95 %. В интервале [M[Х] ± 3s] - 99,73 % (рис. 1.12). Следовательно, почти все результаты измерений лежат в интервале 6s (по три s в каждую сторону от M[Х]). За пределами этого интервала могут находится 0,27 % данных от их общего числа (приблизительно три из тысячи результатов измерений).

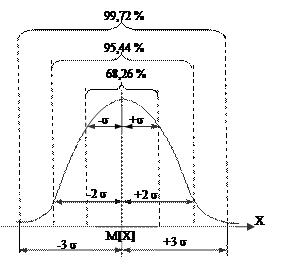
Рис. 1.12. Иллюстрация правила трех сигм

Отсюда следует, что если какое-либо значение величины выходит за пределы ±3s, то с большой вероятностью его можно считать ошибочным.

На основании этого сформулировано правило трех сигм: если при многократных измерениях (n > 25…30) одной и той же величины постоянного размера сомнительный результат Х_сомн отдельного измерения (максимальный или минимальный) отличается от среднего значения более чем на 3s, то с вероятностью 99,7 % он ошибочен, т.е.

если 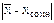> 3s,

то Х_сомн является промахом; его отбрасывают и не учитывают при дальнейшей обработке результатов измерений.

Закон нормального распределения работает при числе результатов измерений n = ¥. В реальности получают конечное число измерений, которые подчиняются закону распределения Стьюдента. При n>25 распределение Стьюдента стремится к нормальному.