Расчет устойчивости при переменных ЭДС
Выше были рассмотрены расчеты устойчивости при постоянстве переходной ЭДС (  = const).
= const).
При коротком замыкании ЭДС 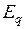 и
и  изменяются во времени в связи с затуханием свободных токов в момент нарушения режима (рис. 4.3, в).
изменяются во времени в связи с затуханием свободных токов в момент нарушения режима (рис. 4.3, в).
Рассматриваемая схема системы представляет неявнополюсный синхронный генератор, имеющий сложную связь с шинами бесконечной мощности, то есть кроме линии связи, например, имеет место промежуточный отбор мощности (рис. 4.12).
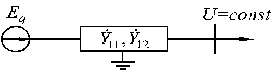
Рис. 4.12. Схема замещения системы
Генератор представляется схемой замещения синхронной ЭДС 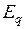 за синхронным сопротивлением
за синхронным сопротивлением 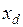 .
.
Для расчетов выдачи мощности генераторов в нормальном и аварийном режимах необходимо определить собственные и взаимные проводимости и углы потерь 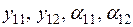 для этих режимов.
для этих режимов.
Расчет динамической устойчивости генератора с учетом переходных электромагнитных процессов требует совместного решения уравнений, определяющих изменения ЭДС 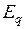 ,
,  и угла
и угла 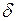 . В этой связи расчет проводят с учетом уравнения переходных процессов в обмотке возбуждения, описанного выше:
. В этой связи расчет проводят с учетом уравнения переходных процессов в обмотке возбуждения, описанного выше:
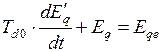 , (4.23)
, (4.23)
где 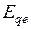 - вынужденная ЭДС.
- вынужденная ЭДС.
В установившемся режиме при неизменном напряжении возбуждения 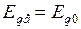 .
.
Уравнение (4.23) содержит две переменные величины 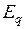 и
и  и для его решения необходимо установить дополнительную связь между этими переменными. Выразив связь между
и для его решения необходимо установить дополнительную связь между этими переменными. Выразив связь между 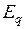 и
и  через собственные и взаимные проводимости системы, величины которых отражают состояние сети при к.з.
через собственные и взаимные проводимости системы, величины которых отражают состояние сети при к.з.
Из векторной диаграммы синхронного генератора имеем:
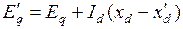 . (4.24)
. (4.24)
Используя выражение (2.45) применительно к рассматриваемой системе выражение для тока 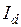 можно записать в виде:
можно записать в виде:
 .
.
Подставляя 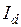 в выражение (4.24), получим:
в выражение (4.24), получим:
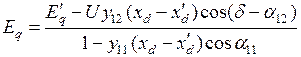 . (4.25)
. (4.25)
Однако уравнение (4.25) содержит еще одну переменную - угол 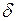 , поэтому уравнения (4.23) и (4.25) решаемы лишь с уравнением относительного движения ротора, которое включает эту переменную
, поэтому уравнения (4.23) и (4.25) решаемы лишь с уравнением относительного движения ротора, которое включает эту переменную
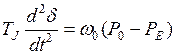 , (4.26)
, (4.26)
где
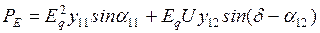 . (4.27)
. (4.27)
Расчет изменения 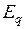 ,
,  и
и 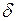 можно провести методом последовательных интервалов в следующей последовательности.
можно провести методом последовательных интервалов в следующей последовательности.
1. Рассчитывают нормальный режим и определяют 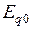 ,
, 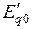 ,
, 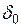 ,
, 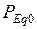 .
.
2. Определяют собственные и взаимные проводимости и углы потерь при к.з. и по уравнению (4.25) определяют 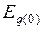 в момент нарушения режима.
в момент нарушения режима.
3. Подставляя 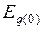 в (4.27), определяют
в (4.27), определяют 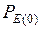 в начале первого интервала и небаланс
в начале первого интервала и небаланс 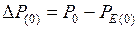 .
.
4. Определяют приращение угла 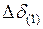 по (4.17) - (4.19) и находят угол в начале второго интервала
по (4.17) - (4.19) и находят угол в начале второго интервала 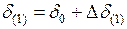 .
.
5. Уравнение (4.23), решенное в конечных разностях, позволяет найти изменение ЭДС  за интервал времени
за интервал времени 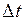 на любом шаге расчета:
на любом шаге расчета:
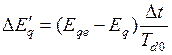 . (4.28)
. (4.28)
Расчет 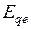 на каждом интервале времени приведен в п. 4.9 по формуле (4.30).
на каждом интервале времени приведен в п. 4.9 по формуле (4.30).
6. Определяют значение  в начале следующего интервала времени:
в начале следующего интервала времени:
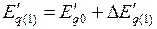 . (4.29)
. (4.29)
7. Определив 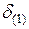 и
и  , можно перейти к расчету следующего интервала, то есть вычислить
, можно перейти к расчету следующего интервала, то есть вычислить 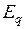 ,
, 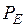 ,
, 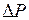 и т.д. Для каждого нового интервала весь расчет повторяется по п.п. 2 - 7.
и т.д. Для каждого нового интервала весь расчет повторяется по п.п. 2 - 7.
В случае наличия в электрической системе явнополюсного генератора его представляют в схеме замещения фиктивной ЭДС 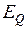 за сопротивлением
за сопротивлением 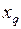 .
.
В уравнениях (4.25) и (4.27) вместо 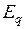 подставляют
подставляют 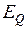 . Но эта ЭДС не может быть использована в уравнении (4.28) для определения
. Но эта ЭДС не может быть использована в уравнении (4.28) для определения 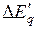 . Чтобы использовать (4.28) необходимо на каждом интервале времени определить синхронную ЭДС
. Чтобы использовать (4.28) необходимо на каждом интервале времени определить синхронную ЭДС 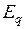 по известной фиктивной ЭДС
по известной фиктивной ЭДС 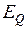 , используя выражение (2.26).
, используя выражение (2.26).
Дата добавления: 2019-09-30; просмотров: 707;











