Движения ротора синхронного агрегата

Вращательное движение ротора генератора характеризуется вторым законом Ньютона:

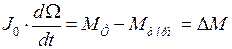, (4.4)

где 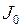- момент инерции турбины и генератора; 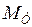- вращающий момент, создаваемый турбиной; 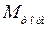- тормозящий момент, определяемый нагрузкой генератора ( 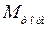= 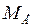); 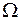- угловая скорость вращения, которая может рассматриваться, как сумма синхронной скорости 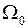и скорости перемещения ротора относительно синхронно вращающейся оси, то есть 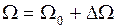; 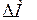- избыток вращающего момента.

Поскольку 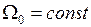, то уравнение (4.4) может быть приведено к виду:

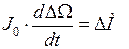. (4.5)

Уравнение (4.5) называют уравнением относительного движения ротора. Приведем его к виду, удобному для использования. Умножив левую и правую части последнего уравнения на 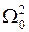, представим его в виде:

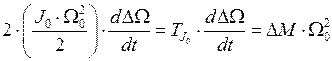, (4.6)

где 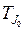- постоянная инерции агрегата, равная удвоенному значению кинетической энергии ротора вращающегося с синхронной скоростью. Она имеет размерность кг×м²×с² или кВт×с (МВт×с).

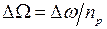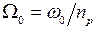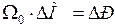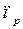Выражение (4.6) можно еще раз преобразовать, перейдя от механической скорости к электрической и от момента - к мощности. Подставив в (4.6) соотношения ; ; , где - число пар полюсов генератора, получим

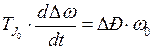, (4.7)

где 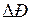- избыточная мощность на валу агрегата в именованных единицах, кВт (МВт).

Разделив правую и левую части (4.7) на базисную мощность, равную номинальной мощности агрегата 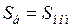, получим избыточную мощность в относительных единицах, постоянную инерции в секундах при номинальных базисных условиях:

,

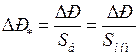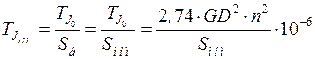, с, (4.8)

где 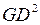- маховый момент (момент вращающихся масс) агрегата, т×м²; 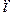- номинальная частота вращения ротора, об/мин; 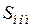- номинальная мощность агрегата, МВ×А.

В (4.8) маховый момент 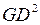равен сумме маховых моментов генератора 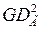и турбины 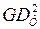, то есть

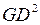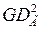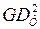= + . (4.9)

При расчетах при базисной мощности, отличной от номинальной, постоянная инерции определяется выражением:

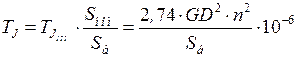. (4.10)

Постоянная инерции эквивалентного агрегата определяется суммой постоянных инерции, приведенных к одной базисной мощности:

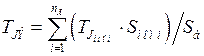, (4.11)

где 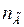- количество агрегатов.

После приведенных преобразований уравнение относительного движения ротора синхронного агрегата можно записать в виде:

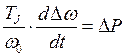, (4.12)

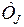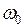где символы, входящие в него, имеют следующие размерности: - с; - 314 рад×с^-1; 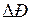- о.е.; 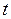- с.

Выразив 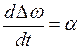, где 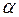- ускорение ротора при относительном движении, то уравнение (4.12) можно записать:

.

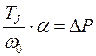Величина ускорения 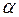может быть определена, как

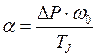. (4.13)

Выразив , ,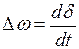

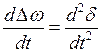а избыточную мощность ,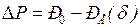

уравнение (4.12) можно записать в виде:

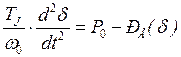, (4.14)

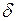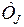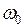где - рад, - с; - 314 рад×с^-1; 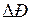- о.е.; 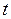- с

или 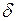- эл.град., 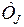- с, 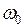= 18000 эл.град×с^-1, 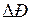- о.е.; 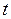- с.

Физический смысл постоянной инерции .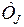

Из (4.12) имеем

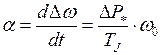
или

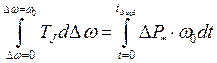при , .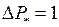

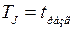Отсюда следует, что постоянная инерции 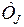численно равна времени разгона ( 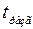), то есть промежутку времени, необходимому для изменения скорости машины от нуля до синхронной при постоянном вращающем моменте (мощности), равном единице.