Практические критерии статической устойчивости
1. Схема электрической системы: эквивалентный генератор в блоке с трансформатором через линию электропередачи работает на шины неизменного напряжения (система "машина-шины") (рис. 1.3, 1.4).
К такой схеме можно прийти от схемы рис. 3.1, приняв к рассмотрению только один генератор и ограничения: 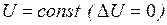 ,
, 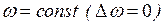 ,
, 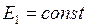 , мощность турбины
, мощность турбины 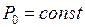 . В этом случае система уравнений (3.2) примет вид:
. В этом случае система уравнений (3.2) примет вид:
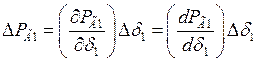 .
.
Обозначив в общем виде 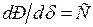 (синхронизирующая мощность), можно определить отклонение угла
(синхронизирующая мощность), можно определить отклонение угла 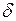 при появлении небаланса мощности:
при появлении небаланса мощности: 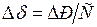 . Согласно последнего выражения можно утверждать, что при
. Согласно последнего выражения можно утверждать, что при 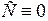 будет наступать предельный (критический) по устойчивости режим, т.к. при ничтожно малом изменении
будет наступать предельный (критический) по устойчивости режим, т.к. при ничтожно малом изменении 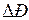 изменение угла
изменение угла 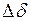 будет получать очень большие значения (
будет получать очень большие значения ( 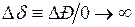 ).
).
Таким образом, критерий предельного (по текучести или сползанию) режима простейшей системы запишется следующим образом:
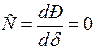 . (3.5)
. (3.5)
Критерием устойчивого режима простейшей системы будет
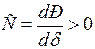 , (3.6)
, (3.6)
то есть все точки на восходящей кривой 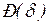 (рис. 2.6). Параметрами предельного режима в данном случае будут амплитудное значение характеристики мощности генератора, определяемое выражением
(рис. 2.6). Параметрами предельного режима в данном случае будут амплитудное значение характеристики мощности генератора, определяемое выражением
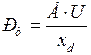
и коэффициент запаса статической устойчивости по активной мощности
 . (3.7)
. (3.7)
Графическое представление критерия приведено на рис. 2.6. Для суждения об устойчивости по предлагаемому критерию необходимо рассчитать параметры установившегося режима и определить 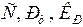 .
.
2. Две станции (два эквивалентных генератора), соизмеримые по мощности, работают на общую нагрузку.
Расчетная схема и схема замещения соответствуют рис. ____, а, в. Предельный по устойчивости режим предполагается при следующих ограничениях 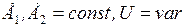 , в точке с
, в точке с 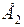 предполагаются как шины неизменного напряжения, частота в системе принимается постоянной (
предполагаются как шины неизменного напряжения, частота в системе принимается постоянной ( 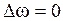 ), нагрузка представляется постоянным сопротивлением
), нагрузка представляется постоянным сопротивлением 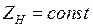 (рис. ___, в).
(рис. ___, в).
При постоянной выдаваемой мощности 2-й станцией и росте нагрузки 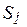 , мощность, выдаваемая 1-й станцией будет увеличиваться, в результате может иметь место превышение предела передаваемой мощности от первой станции и нарушение устойчивости. В этом случае, как и в предыдущем, целесообразно применять критерий
, мощность, выдаваемая 1-й станцией будет увеличиваться, в результате может иметь место превышение предела передаваемой мощности от первой станции и нарушение устойчивости. В этом случае, как и в предыдущем, целесообразно применять критерий 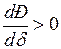 или
или 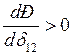 , где
, где 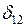 - угол между
- угол между 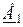 и
и 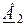 .
.
Мощность, выдаваемая от станции в систему:
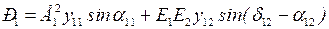 .
.
Предельный по устойчивости режим определяется по условию:
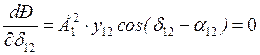 .
.
Критерий устойчивости
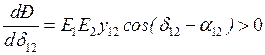 . (3.8)
. (3.8)
Амплитуда характеристики мощности генератора (предел передаваемой мощности) от станции 1:
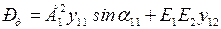 .
.
Коэффициент запаса статической устойчивости по активной мощности:
 . (3.9)
. (3.9)
Расчет установившегося режима для определения критерия (определение ЭДС станций, проводимостей, углов потерь) проводят аналогично с расчетом установившегося режима сложных систем. Для графического представления критерия можно использовать рис. ___.
3. Многомашинная система, питающая узловую точку с 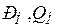 .
.
Расчетная схема рассматриваемой системы и ее схема замещения представлены на рис. 3.2, а, б.
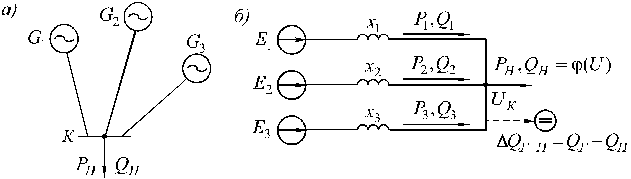
Рис. 3.2. Исследуемая схема системы (а), схема замещения системы (б)
Практический критерий статической устойчивости режима такой системы можно сформулировать при следующих ограничениях: неизменная частота ( 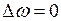 ); сохранение баланса активной мощности в узле К и генерируемой мощности (
); сохранение баланса активной мощности в узле К и генерируемой мощности ( 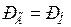 ) при нарушении баланса по реактивной мощности; постоянство ЭДС генераторов (станций)
) при нарушении баланса по реактивной мощности; постоянство ЭДС генераторов (станций) 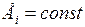 .
.
В этом случае неустойчивость системы обусловлена изменением напряжения в узле К 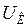 при нарушении баланса реактивной мощности в узле
при нарушении баланса реактивной мощности в узле
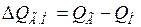 ,
,
где 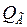 - суммарная генерируемая реактивная мощность в узле;
- суммарная генерируемая реактивная мощность в узле;
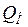 - реактивная мощности нагрузки.
- реактивная мощности нагрузки.
Изменения (неустойчивость) напряжения в точке К системы могут быть выявлены при помощи построения зависимостей реактивной мощности нагрузки и генераторов от напряжения, то есть 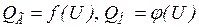 (рис. 3.3). Зависимость
(рис. 3.3). Зависимость 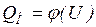 представляет собой обычную статическую характеристику, а
представляет собой обычную статическую характеристику, а 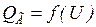 можно получить по выражению реактивной мощности у шин приемника
можно получить по выражению реактивной мощности у шин приемника
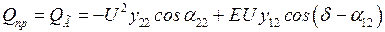 .
.
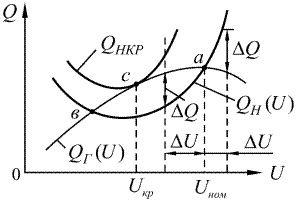
Рис. 3.3. Устойчивый, критический и неустойчивый режимы системы
При неучете активных сопротивлений в цепи статора каждого из генераторов 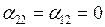 . В этом случае
. В этом случае
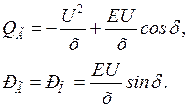
При 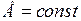 задаются различными напряжениями
задаются различными напряжениями 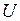 , определяют
, определяют  по статической характеристике
по статической характеристике 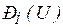 и находят углы
и находят углы 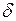 , а затем определяют
, а затем определяют 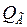 , используя последние выражения. Построенные зависимости
, используя последние выражения. Построенные зависимости 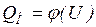 и
и 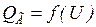 (рис. 3.3) могут иметь или две точки пересечения
(рис. 3.3) могут иметь или две точки пересечения 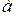 и
и 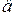 , характеризующие два возможных состояния равновесия системы, или одно точку касания (точка
, характеризующие два возможных состояния равновесия системы, или одно точку касания (точка 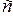 ), характеризующую критический режим.
), характеризующую критический режим.
Предельный (критический) по устойчивости режим согласно (3.4) при принятых ограничениях и рассматриваемой схеме системы определяется выражением:
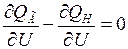 .
.
Учитывая, что дифференцирование происходит по одной переменной, запишем:
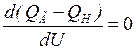 или
или 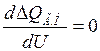 . (3.10)
. (3.10)
Выражение (3.10) является критерием предельного режима. Этот режим имеет место при увеличении реактивной мощности нагрузки, когда у характеристик мощности 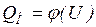 и
и 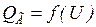 имеется лишь одна общая точка
имеется лишь одна общая точка 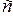 , при этом напряжение в узле нагрузки будет равно критическим
, при этом напряжение в узле нагрузки будет равно критическим 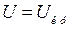 . В точке
. В точке 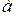 , когда
, когда 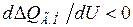 , система устойчива; в этом случае при любом случайном отклонении напряжения на
, система устойчива; в этом случае при любом случайном отклонении напряжения на 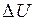 (рис. 3.3) появляется избыток реактивной мощности
(рис. 3.3) появляется избыток реактивной мощности 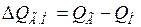 , стабилизирующее напряжение узла нагрузки.
, стабилизирующее напряжение узла нагрузки.
Таким образом, критерием устойчивости режима системы является выражение
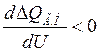 . (3.11)
. (3.11)
Очевидно, что точка 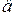 - точка неустойчивого состояния равновесия.
- точка неустойчивого состояния равновесия.
Запас устойчивости системы по напряжению определяется выражением вида:
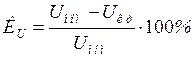 . (3.12)
. (3.12)
Повышение статической устойчивости нагрузки достигается уменьшением реактивного сопротивления (включением дополнительных ЛЭП, трансформаторов) и увеличением ЭДС генераторов (при отключении ЛЭП, трансформаторов и т.д.).
Уменьшение реактивной мощности нагрузки также повышается устойчивость, но следует иметь ввиду, что компенсация реактивной мощности нагрузки, широко осуществляемая конденсаторными батареями (КБ), приводит к снижению устойчивости системы. Это объясняется тем, что при снижении 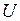 в узле нагрузки выдача реактивной мощности
в узле нагрузки выдача реактивной мощности 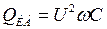 уменьшается, что приводит к еще большему понижению напряжения. Процесс снижения
уменьшается, что приводит к еще большему понижению напряжения. Процесс снижения 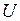 может иметь лавинообразный характер за счет опрокидывания асинхронных двигателей.
может иметь лавинообразный характер за счет опрокидывания асинхронных двигателей.
В удаленных узлах системы для компенсации 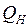 целесообразно применять синхронные компенсаторы (СК) и синхронные двигатели (СД) с форсированием возбуждения. При понижении напряжения реактивная мощность СК за счет форсировки возбуждения возрастает, что позволяет стабилизировать напряжение и не допускать его лавины.
целесообразно применять синхронные компенсаторы (СК) и синхронные двигатели (СД) с форсированием возбуждения. При понижении напряжения реактивная мощность СК за счет форсировки возбуждения возрастает, что позволяет стабилизировать напряжение и не допускать его лавины.
4. Станция (эквивалентный генератор), питающая через ЛЭП комплексную нагрузку соизмеримой мощности.
Комплексная нагрузка в узле рассматриваемой электрической системы включает синхронные двигатели, освещение, асинхронные двигатели (более 50 % от общего состава нагрузки) и др. В этом случае для решения вопроса об устойчивости системы оценивается устойчивость узла комплексной нагрузки и в первую очередь устойчивость асинхронных двигателей.
Для получения критериев рассматриваемой системы принимают следующие ограничения: не учитывают изменения частоты ( 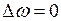 ); ЭДС эквивалентного генератора принимают постоянной (
); ЭДС эквивалентного генератора принимают постоянной ( 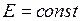 ); нагрузка узла представлена статическими характеристиками
); нагрузка узла представлена статическими характеристиками 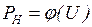 ,
,  (рис. 2.19, а) или заданных в виде таблицы данных.
(рис. 2.19, а) или заданных в виде таблицы данных.
Схема замещения рассматриваемой системы после эквивалентирования изображена на рис. 3.4. Для такой схемы напряжение на шинах нагрузки и эквивалентная ЭДС связаны выражением:
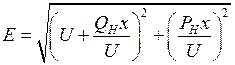 . (3.13)
. (3.13)
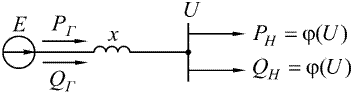
Рис. 3.4. Схема замещения упрощенной системы
Задаваясь различными значениями напряжения 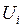 находят
находят 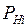 и
и 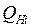 по статическим характеристикам, а по (3.13) находят
по статическим характеристикам, а по (3.13) находят 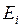 и строят зависимости
и строят зависимости 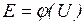 (рис. 3.5). Характер этой зависимости существенно зависит от наличия в составе нагрузки асинхронных двигателей. При данной ЭДС генераторов
(рис. 3.5). Характер этой зависимости существенно зависит от наличия в составе нагрузки асинхронных двигателей. При данной ЭДС генераторов 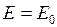 возможные режимы на характеристике
возможные режимы на характеристике 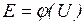 определяются точками
определяются точками 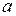 и
и 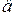 . Точка
. Точка 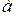 , в которой
, в которой  , соответствует достаточно высокому и "жесткому" напряжению на шинах нагрузки, при котором асинхронные двигатели работают устойчиво. Напряжение, соответствующее точке
, соответствует достаточно высокому и "жесткому" напряжению на шинах нагрузки, при котором асинхронные двигатели работают устойчиво. Напряжение, соответствующее точке 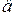 мало и недостаточно для устойчивой работы двигателей. Если кривая
мало и недостаточно для устойчивой работы двигателей. Если кривая 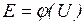 лишь касается линии ЭДС
лишь касается линии ЭДС 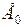 (точка
(точка 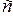 ), то имеет место критическое напряжение
), то имеет место критическое напряжение 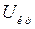 , при котором
, при котором 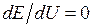 .
.
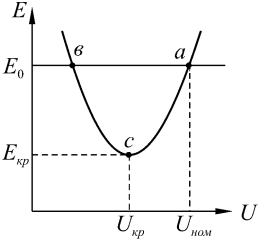
Рис. 3.5. Графическое представление критерия
Таким образом, для рассматриваемой схемы системы критерий устойчивого режима
 , (3.14)
, (3.14)
критерий предельного режима
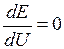 , (3.15)
, (3.15)
коэффициент запаса статической устойчивости по напряжению узла
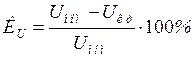 . (3.16)
. (3.16)
5. Эквивалентный асинхронный двигатель, питающийся от мощной системы.
В этом случае предполагается, что система обладает бесконечной мощностью по сравнению с мощностью эквивалентного двигателя и имеет узловую точку с неизменным напряжением или точку эквивалентного источника с неизменной ЭДС. Напряжение на зажимах двигателя и для конкретного режима постоянно ( 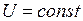 ).
).
Расчетная схема и схема замещения системы показаны на рис. 2.14 и 2.15, б соответственно.
На рис. 3.6 представлены статические характеристики потребляемой активной мощности в функции скольжения при различных постоянных напряжения 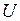 . Характеристики рассчитаны по выражению (2.47). Амплитуда характеристики
. Характеристики рассчитаны по выражению (2.47). Амплитуда характеристики  пропорциональна квадрату напряжения
пропорциональна квадрату напряжения 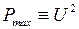 и при понижении напряжения резко падает.
и при понижении напряжения резко падает.
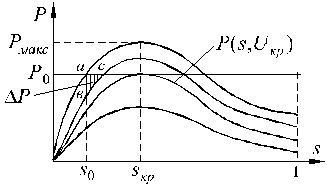
Рис. 3.6. Статические характеристики асинхронного двигателя
При неизменной мощности приводного механизма  на валу двигателя возникает избыток мощности
на валу двигателя возникает избыток мощности 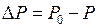 , соответствующий отрезку
, соответствующий отрезку 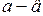 , скольжение двигателя
, скольжение двигателя 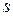 возрастает и в точке
возрастает и в точке 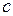 устанавливается стационарный режим. Если
устанавливается стационарный режим. Если  , то двигатель теряет устойчивость, опрокидывается и останавливается. Устойчивость двигателя обеспечивается лишь на восходящей ветви характеристики мощности.
, то двигатель теряет устойчивость, опрокидывается и останавливается. Устойчивость двигателя обеспечивается лишь на восходящей ветви характеристики мощности.
Таким образом, можно сформулировать критерий статической устойчивости асинхронного двигателя:
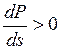 , (3.17)
, (3.17)
критерий предельного режима 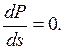
Запас статической устойчивости по мощности:
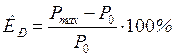 . (3.18)
. (3.18)
Можно определить запас устойчивости по напряжению и скольжению.
Используя (2.47) из условия

находят так называемое "критическое скольжение" 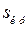 , то есть скольжение, при котором
, то есть скольжение, при котором 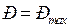 :
:
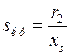 . (3.19)
. (3.19)
Подставляя 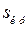 в (2.47) вместо
в (2.47) вместо 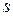 , определим амплитуду характеристики мощности, так называемую предельную из условия устойчивости мощности
, определим амплитуду характеристики мощности, так называемую предельную из условия устойчивости мощности
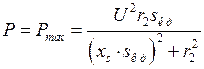 .
.
Используя (3.19) из последнего выражения получим:
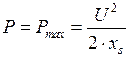 .
.
При некотором критическом напряжении 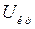 максимальная мощность (момент)
максимальная мощность (момент) 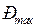 становится равным мощности (моменту) приводного механизма
становится равным мощности (моменту) приводного механизма 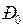 (рис. 3.6):
(рис. 3.6):
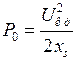 ,
,
откуда
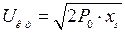 . (3.20)
. (3.20)
Запасы устойчивости двигателя по напряжению и скольжению определяются по формулам:
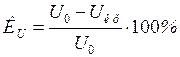 ;
; 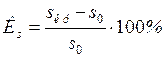 . (3.21)
. (3.21)
6. Эквивалентный асинхронный двигатель получает питание через ЛЭП от эквивалентного генератора (станции) соизмеримой мощности.
Расчетная схема такой системы имеет вид, приведенный на рис. 3.7.
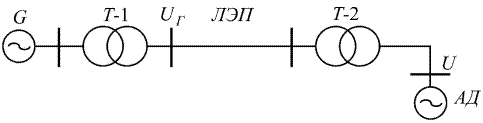
Рис. 3.7. Расчетная схема системы
После эквивалентирования, замены сопротивлений трансформаторов, ЛЭП внешним сопротивлением 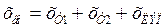 и переноса
и переноса 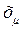 в схеме замещения двигателя к месту присоединения ЭДС
в схеме замещения двигателя к месту присоединения ЭДС 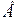 , получим упрощенную схему замещения системы, изображенной на рис. 3.8.
, получим упрощенную схему замещения системы, изображенной на рис. 3.8.
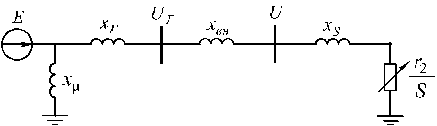
Рис. 3.8. Упрощенная схема замещения системы
Расчет статической устойчивости асинхронного двигателя для такой системы может быть проведен по формулам (2.47), (3.17)-(3.21) при подстановке вместо 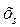 эквивалентного сопротивления
эквивалентного сопротивления 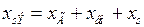 , а вместо напряжения
, а вместо напряжения 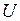 - ЭДС эквивалентного генератора
- ЭДС эквивалентного генератора 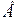 . Кроме того, сопротивление генератора
. Кроме того, сопротивление генератора 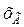 принимают в зависимости от расчетной ЭДС (
принимают в зависимости от расчетной ЭДС ( 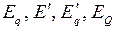 ,
, 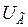 ). При представлении генератора ЭДС
). При представлении генератора ЭДС 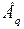 -
- 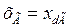 ; при
; при 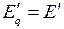 -
- 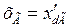 ; при
; при 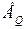 -
- 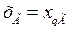 ; а если
; а если 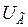 , то
, то 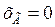 .
.
Дата добавления: 2019-09-30; просмотров: 1228;











