Комплексные сопротивления системы вибраторов.

Рассмотрим систему, состоящую из 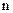связанных между собой излучателей. Для них можно записать следующую систему уравнений:

,

,

.

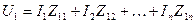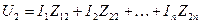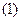
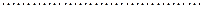
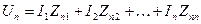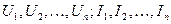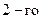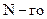Здесь - комплексные напряжения и токи на зажимах , и вибраторов.

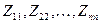- собственные сопротивления на зажимах 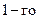, 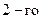и т.д. вибраторов.

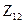- взаимное сопротивление между 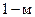и 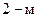вибраторами; 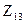- взаимное сопротивление между 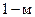и 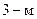вибраторами и т.д.

Взяв отношение 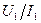в первом из равенств 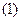, получим значение эквивалентного входного сопротивления на зажимах 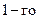вибратора:

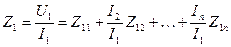
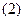
Подобные же выражения получаются и для других вибраторов. Полное комплексное сопротивление можно представить в виде суммы собственного сопротивления 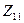и сопротивления 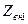, вносимого остальными вибраторами в первый

,

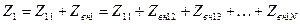где

; ;

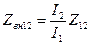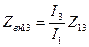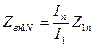
При равенстве токов вносимое сопротивление становится равным взаимному.

Например, 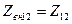при 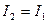, а при .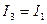

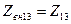Таким образом, взаимным сопротивлением двух вибраторов можно назвать сопротивление, которое вносится 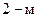вибратором в 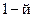(или наоборот), в случае, когда токи обоих вибраторов одинаковы по фазе и по амплитуде.

Из системы уравнений 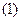видно, что при заданных напряжениях на зажимах вибраторов и известных значениях собственных и взаимных сопротивлений могут быть определены все токи вибраторов. Если же токи вибраторов определены или заданы заранее, тогда с помощью выражений 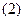могут быть найдены полные комплексные сопротивления вибратора.