Эта формула связывает мощность излучения с квадратом тока через сопротивление излучения.
Для определения воспользуемся методом вектора Пойнтинга. В соответствии с этим методом симметричный вибратор окружается сферой радиусом 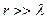 , центр сферы совпадает с центром симметричного вибратора.
, центр сферы совпадает с центром симметричного вибратора.
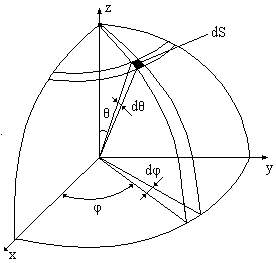
Рис. 21. Сферические координаты площадки излучения
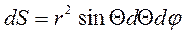
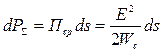
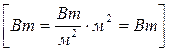
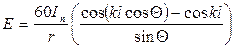
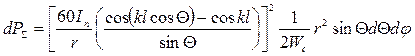
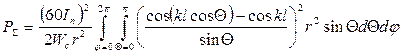
Полагая 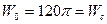
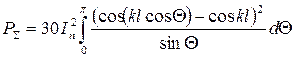
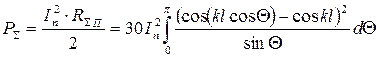
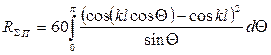
После интегрирования получается формула, которую в 1924 году получил Баллангайн.
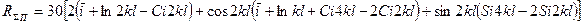 ,
,
где 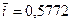 постоянная Эйлера
постоянная Эйлера
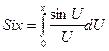 – интегральный синус
– интегральный синус
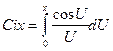 – интегральный косинус
– интегральный косинус
(См. в Янке Е., Эмде Ф. «Специальные функции»)
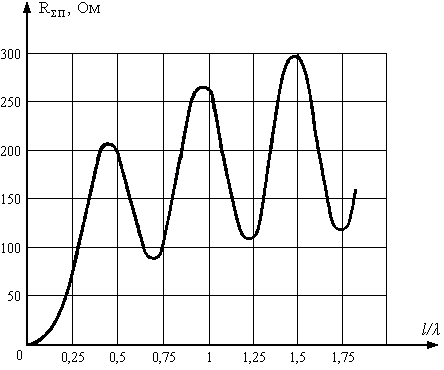
Рис. 22.Сопротивление излучения тонкого симметричного вибратора, отнесенное к току в пучности, в зависимости от 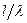
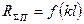
если 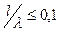 , то
, то 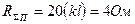
если 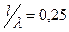 , то
, то 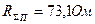
Входное сопротивление симметричного вибратора.
Мощность, подведенная от генератора к симметричному вибратору делится на излучаемую, теряемую в самом вибраторе (омические потери, потери в изоляторах, окружающих металлический проводник и в земле).
Излучаемая мощность характеризуется сопротивлением излучения 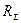 .
.
Мощность потерь характеризуется сопротивлением 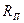 .
.
Кроме излученного поля, есть еще колеблющееся вблизи антенны. Этому полю соответствует реактивная мощность. Эта мощность, то отдается генератором в пространство, то принимается генератором.
Реактивная мощность характеризуется реактивным сопротивлением 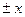
Таким образом
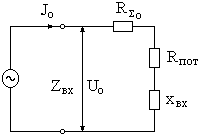
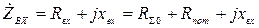
для симметричного вибратора, как правило 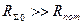 , тогда
, тогда
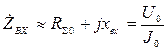
Рассмотрим полуволновой вибратор ( 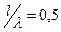 ).
).
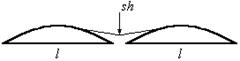
Расчет ведут следующим образом. В вибраторе существуют потери, пусть 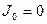 , тогда
, тогда 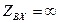 , но этого не может быть, так как
, но этого не может быть, так как 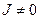 в точке питания он конечен, значит и
в точке питания он конечен, значит и 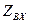 – конечно.
– конечно.
Закон синуса тока – справедлив для линии без потерь, а у нас существуют потери, значит закон не синусоидальный, а такой, какой бывает в линиях с потерями. Он соответствует закону гиперболического синуса:
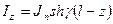
где 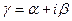 ,
, 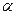 – коэффициент затухания и
– коэффициент затухания и 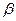 – коэффициент фазы.
– коэффициент фазы.
Поэтому при расчете 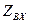 «коротких» вибраторов (
«коротких» вибраторов ( 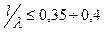 и
и 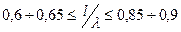 ), то есть у которых узел тока находится от точек питания вибратора не ближе
), то есть у которых узел тока находится от точек питания вибратора не ближе 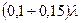 , исходят из синусоидального распределения тока.
, исходят из синусоидального распределения тока.
При расчете 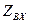 «длинных» вибраторов (
«длинных» вибраторов ( 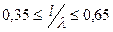 ) следует исходить из распределения тока по закону
) следует исходить из распределения тока по закону 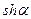 .
.
Найдем формулу для расчета активной составляющей 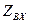
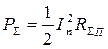 через ток в пучности
через ток в пучности
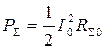 через ток в точках запитки
через ток в точках запитки
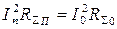
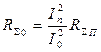
Используя 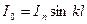
 , получим
, получим
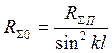
Значение 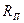 для данной длины находят из таблиц или графиков
для данной длины находят из таблиц или графиков
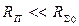 для
для 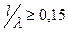
При расчете 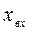 пользуются формулой входного сопротивления разомкнутой на конце двухпроводной линии без потерь, заменяя в ней волновое сопротивление линии волновым сопротивлением антенны (симметричного вибратора)
пользуются формулой входного сопротивления разомкнутой на конце двухпроводной линии без потерь, заменяя в ней волновое сопротивление линии волновым сопротивлением антенны (симметричного вибратора)
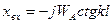
Таким образом
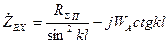 (7)
(7)
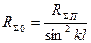
Дата добавления: 2017-03-12; просмотров: 2763;











