Разбивка кривых на местности

Разбивка главных точек кривой. Закрепив на местности вершину угла и предшествующие ему пикеты, закрепляют главные точки кривой.

Середину кривой СК закрепляют, отложив от ВУ по направлению биссектрисы отрезок, равный Б (или Б_с).

На новом после вершины угла направлении трассы откладывают величину домера, после чего продолжают разбивку пикетажа. Обеим точкам домера (его началу и концу) присваивают одно и то же пикетажное наименование, благодаря чему пикетаж точки КК совпадает с пикетажем, считаемым по кривой.

Положение начала кривой НК и конца кривой КК определяют, используя разбитый пикетаж. Например, если ПК НК = 5 + 39,27, то от пикета № 5 откладывают вперёд 39,27 м и здесь колышком и сторожком закрепляют точку НК.

Детальная разбивка кривых.При детальной разбивке кривую закрепляют на местности через 10 или 20 м, применяя разные способы.

Способ ординат от касательной для круговой кривой. Для каждой точки i (рис. 15.7, а), задавая расстояние k от начала кривой, вычисляют ее координаты:

x = R sinj; y = R (1 – cosj). (15.10)

Здесь угол j выражен в радианах и равен j = k/R.

Разбивку кривой ведут от ее начала и от конца к середине. Мерной лентой по оси x откладывают длину кривой k, от полученной точки отступают назад на величину k–x и здесь строят перпендикуляр – ординату y. Значения k–x и y обычно выбирают из таблиц для разбивки кривых.

а) б) в)

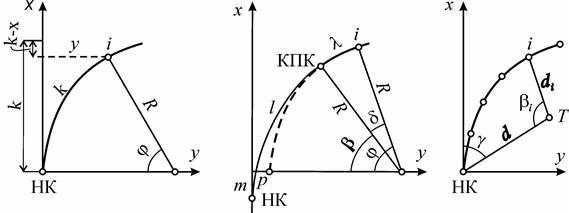
Рис. 15.7 Детальная разбивка кривых:

а – способом ординат от касательной для круговой кривой;

б – то же, для переходной и следующей за ней круговой кривой;

в – разбивка кривой электронным тахеометром

Способ ординат от касательной для переходной и следующей за ней круговой кривой (рис. 15.7, б). Для точек, расположенных в пределах переходной кривой, то есть при k £ l, координаты x, y вычисляют по формулам (15.8) и (15.9), принимая s = k. Для точек i, расположенных на круговой кривой, где k > l, вычисления выполняют по формулам:

l = k – l; d = l/R; j = b + d;

x = m + R sinj; y = p + R (1 - cosj). (15.11)

Действия при разбивке кривой на местности аналогичны тем, что выполняют при разбивке круговой кривой.

Разбивка кривой с помощью электронного тахеометра. Выбирают на местности такую точку T (рис. 15.7, в), где обеспечена видимость точек будущей кривой и ее начала НК. В точке НК измеряют угол g и расстояние d. Вычисляют координаты точки Т:

x_T = d cosg; y_T = d sing.

По приведенным выше формулам вычисляют координаты точек кривой x_i, y_i (i = 1, 2, …).

Электронный тахеометр устанавливают в точке Т. Зная координаты точек Т, НК и i, вычисляют разбивочные элементы - углы b_i и расстояния d_i. Построив тахеометром вычисленные углы и расстояния, находят и закрепляют положение точек кривой на местности.