ВЫНУЖДЕННОМ ТЕЧЕНИИ В КАНАЛАХ

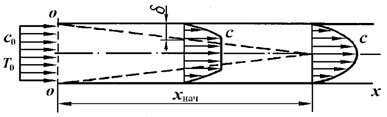
Схема течения. Рассмотрим случай, когда течение происходит в круглой трубе, причем скорость и температура потока на входе в трубу равномерны по сечению (рис. 2.6). На стенках трубы, через которую течёт теплоноситель, образуется пограничный слой (штриховые линии), который может быть ламинарным или турбулентным. Толщина пограничного слоя на стенке трубы увеличивается по длине канала и на некотором расстоянии от входного сечения х_нач он смыкается, т.е. заполняет все поперечное сечение канала. Начиная с этого сечения, устанавливается стабильное (неизменное) распределение скорости теплоносителя по сечению потока. Отрезок длинною х_нач от начала трубы до этого сечения называется начальным участком или участком стабилизации.

На начальном участке меняется и профиль температур. Если во входном сечении поток имеет постоянную по сечению температуру, то по мере удаления от входа в теплообмен вовлекаются все новые слои, пока не установится характерный профиль температуры, который зависит от направления теплового потока (рис. 7.7).

Рис. 2.6

Режим течения. При анализе теплоотдачи в круглых трубах за характерный размер принимают внутренний диаметр канала d. Поэтому критерии Nu и Re имеют вид:

, ,

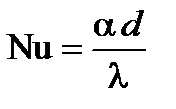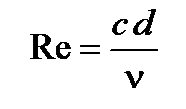где с = G /Fr - средняя скорость теплоносителя по сечению канала, G – расход газа через канал, F – площадь поперечного сечения канала,r - средняя плотность теплоносителя в данном сечении канала.

Режим течения теплоносителя в трубе зависит от значения числа Рейнольдса. При числах Re < 2300 течение всегда ламинарное, а при Re > 1,5×10⁵ турбулентный пограничный слой начинает формироваться практически с входного сечения.

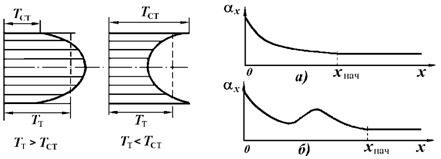
Изменение a по длине трубы определяется изменением толщины и структуры пограничного слоя. Если на начальном участке режим течения в пограничном слое остается неизменным, то по мере роста толщины пограничного слоя, а следовательно, и теплового сопротивления, коэффициент a_х монотонно уменьшается, достигая минимального значения при х = x_нач(рис. 2.7б); при

х > x_нач значение a_х остается постоянным.

Если же на начальном участке режим течения в пограничном слое изменяется, то в зоне перехода от ламинарного режима течения к турбулентному происходит увеличение коэффициента теплоотдачи с последующим снижением, обусловленным ростом толщины уже турбулентного пограничного слоя.

а) б)

Рис. 2.7

Плотность теплового потока; критериальные уравнения. При течении в каналах, как и при внешнем обтекании, плотность теплового потока определяется по уравнению Ньютона 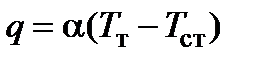, в котором T_T - средняя по сечению канала температура (рис. 2.7а). Эта температура в общем случае изменяется по длине трубы и может быть определена из уравнения ,

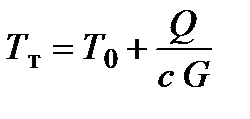где G , c , Т₀ - расход, теплоемкость (для газа c = c_р) и температура теплоносителя на входе в канал; Q - тепловой поток на участке от входа до рассматриваемого сечения.

Местный коэффициент теплоотдачи определяется из критериального уравнения, которое в данном случае имеет вид:

,

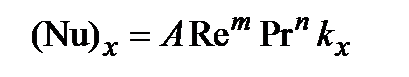где k_x - коэффициент, учитывающий изменение a_х на начальном участке.

Значения коэффициентов А, m, n и k_x в этом уравнении зависят от режима течения, причём согласно результатам экспериментов при ламинарном течении ,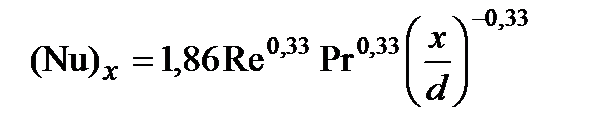

где длина начального участка составляет 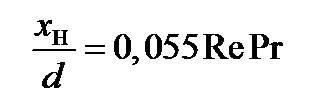и если х >х_н, то в эту формулу надо подставлять х = х_н, а при турбулентном течении

,

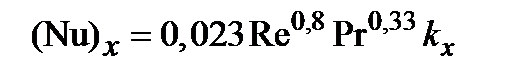где 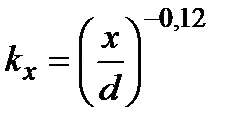и при 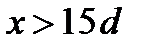следует принимать k_х=1.

Замечания:

1. Приведенные выше критериальные уравнения получены при экспериментальном исследовании теплоотдачи при течении в круглых трубах. С достаточной для многих инженерных задач точностью их можно применять и для каналов иных форм. Для этого при определении коэффициента теплоотдачи в таких каналах в критериальных уравнениях в качестве линейного размера следует принимать значение так называемого эквивалентного диаметра 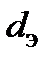, равного диаметру круглой трубы, имеющей то же отношение площади проходного сечения 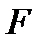к периметру 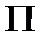, омываемому теплоносителем. 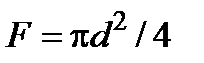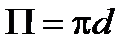Так как у круглой трубы и , то .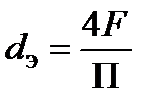

Например, для канала прямоугольной формы со сторонами и .

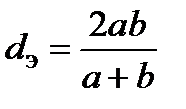2. Приведенные выше уравнения относятся к гладким трубам. Если стенки каналов имеют заметную шероховатость (высота бугорков больше толщины ламинарного подслоя) или снабжены специальными турбулизаторами, то интенсивность теплоотдачи будет более высокой, что учитывается с помощью специальных поправочных коэффициентов.

3. В указанных уравнениях физические свойства теплоносителя приняты постоянными. Однако, когда температурный напор DТ = Т_т - Т_ст велик, физические свойства теплоносителя (теплоёмкость, коэффициенты l и m) могут значительно изменяться по сечению и по длине канала. Для приближённого учёта этого влияния физические свойства теплоносителя, используемые при определении критериев подобия, принято определять по эффективной температуре Т_эф , значение которой находится между Т_т и Т_ст . В этом случае критериальное уравнение записывают так: .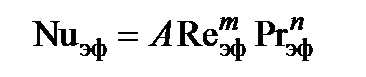

При небольших скоростях движения теплоносителя можно принимать

.

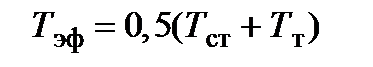Факторы, влияющие на коэффициент теплоотдачи. Решим критериальное уравнение относительно местного коэффициента теплоотдачи a_х . Учитывая выражения для критериев Re и Pr после соответствующих преобразований получим ,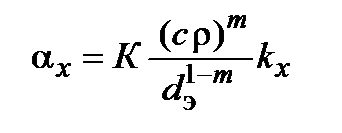

где .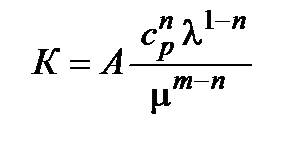

Видно, что местный коэффициент теплоотдачи a_х зависит от режима течения теплоносителя (А, т, n), от плотности тока ( 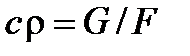), значения эквивалентного диаметра в рассматриваемом сечении канала и от физических свойств теплоносителя.