Методы «свободной геометрии». Сплайн-трассирование

В условиях автоматизированного проектирования, когда любое проектное решение требует формализованного представления информации в числовом или аналитическом виде, а оценка этих решений связана, как правило, с функциональным анализом, значимость выбора подходящих интерполирующих и аппроксимирующих функций возрастает. Наиболее подходящими функциями для этого являются сплайны как универсальный математический аппарат для описания, хранения, преобразования, анализа и представления геометрических форм элементов, в первую очередь, трасс проектируемых автомобильных дорог.

Термин «сплайн» (spline-англ.) происходит от названия чертежного инструмента - тонкой металлической или деревянной линейки, которая изгибается так, чтобы проходить через заданные точки {х_i, у_i = f(x)} (рис. 28.7).

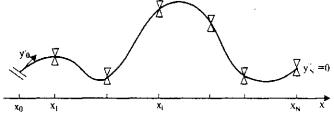
Рис. 28.7. Очертание сплайна как математического аналога гибкой линейки

Теория сплайнов, получившая распространение в 60-е годы, прошла этап бурного развития. В настоящее время сплайны, наряду с классическими многочленами, признаны стандартными функциями математического анализа. Их широкое применение в промышленных технологиях связано с тем, что сплайны имеют хорошие аппроксимативные свойства и, в то же время, чрезвычайно просты и удобны для построения вычислительных алгоритмов на компьютере.

Применимость сплайнов в дорожном проектировании активно исследовалась едва ли не с самого зарождения теории сплайнов (В.А. Федотов, В.Ю. Голубин, В. Кюн, В. Фулчик и др.). Ряд программных разработок для автоматизированного трассирования автомобильных дорог в плане и продольном профиле на основе сплайнов нашли применение в проектной практике. Заметим, что сплайн-трассы никоим образом не связаны с тангенциальным ходом и их разбивка на местности может осуществляться от произвольных базисов (рис. 28.8).

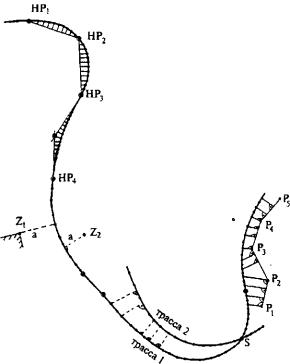
Рис. 28.8. Возможные схемы разбивки сплайн-трасс

Из всего многообразия сплайнов в данной работе рассматриваются, в первую очередь, алгебраические сплайны 1-й и 3-й степеней - интерполяционные и сглаживающие. Выбор алгебраических сплайнов обусловлен тем, что они наиболее экономичны с вычислительной точки зрения и обладают достаточными свойствами аппроксимации и гладкости.

Сплайны 1-й степени (линейные) служат, во-первых, хорошей и доступной иллюстрацией к пониманию процессов построения сплайновых алгоритмов, а, во-вторых, достаточны для описания геометрических элементов дорог, представляемых в виде ломаных линий (магистральные и тангенциальные ходы, продольные и поперечные профили земли и т.д.).

Построению гладких кривых служат сплайны 3-й степени (кубические), которые вместе со своими первой и второй производными несут проектировщику необходимую количественную и качественную информацию о проектируемой трассе.

Сплайны можно определить двумя способами: исходя из взаимного согласования простых функций (многочленов невысокой степени) и из решения задачи минимизации.

К сплайнам, определяемым по первому способу, можно отнести интерполяционные сплайны, которые необходимы для аналитического представления дискретно заданной информации.

Сглаживающие сплайны определяют чаще на основе второго способа. Именно сглаживающие сплайны находят самое широкое применение для оптимизации тех проектных решений, которые на начальной стадии рассмотрения носят, как правило, приближенный характер.

Кубическая интерполяционная сплайн-функция на каждом интервале между узлами интерполяции записывается уравнением вида:

S = f_i + B_i(x - x_i) + C_i(x - x_i)² + D_i(x - x_i)³, x_i £ х £ x_i+1.

Недостатком такого вида записи является то, что отсутствует возможность изменения формы сплайн-функции на участке между двумя жестко закрепленными интерполяционными точками. Лишь перемещением одной из точек (узлов) интерполяции можно добиться некоторого изменения формы сплайн-кривой.

Более гибкими возможностями в этом смысле обладают рациональные сплайны, непрерывные вместе со своими первой и второй производными:

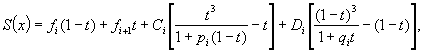где

t = (x - x_i)/h_i, h_i = x_i+1 - x_i, р_i, q_i - заданные числа, - 1 < р_i, q_i < ¥.

Из уравнения рационального сплайна видно, что при р_i = q_i = 0, i = 0,1,..., N-1, рациональный сплайн превращается в обычный кубический сплайн. Кроме того, можно считать, что сплайн первой степени также является частным случаем кубического сплайна, поскольку при всех р_i, q_i ®¥, i = 0,1,...,N-1, справедливо S(x) ® f_i(1 - t) + f_i+1t, х Î [x_i, x_i+1]. Таким образом, можно ожидать, что при использовании рациональных сплайнов путем надлежащего выбора свободных параметров р_i, q_i достигается высокая точность приближения на участках достаточной гладкости интерполируемой функции, а на участках с большими градиентами сплайн отвечает требованиям качественного характера - выпуклости и монотонности.

«Слабым» местом в обосновании интерполяционных сплайнов как универсального математического аппарата при трассировании автомобильных дорог является допущение (условие), что вершины интерполяции назначены проектировщиком верно и при вычислении значений самого сплайна корректировке не подлежат.

Проанализируем, как на практике назначают местоположение вершин. Если трассирование выполняют на основе карты или топографического плана, то проводят эскизную линию дороги, которая, по мнению проектировщика, является наиболее целесообразной при заданных условиях, «от руки» или с помощью механических приспособлений. Далее на эскизной линии фиксируют вершины интерполяции и замеряются их координаты. При этом не существует строго формализованных алгоритмов назначения местоположения вершин, есть лишь ряд практических советов. В частности, частое расположение вершин приводит к осцилляции кривизны такого сплайна ввиду неизбежной погрешности съемки координат вершин интерполяции; редкое их расположение вызывает существенные отклонения сплайн-трассы от порождающей ее эскизной линии.

Если трассирование выполняют по материалам полевых изысканий, то вершинами сплайн-интерполяции в этом случае являются съемочные точки цифровой модели местности и погрешность в установлении их координат еще более очевидна ввиду наличия ошибок случайного и систематического характера.

Хорошего приближения сплайн-трассы к эскизному варианту и, в то же время, достаточной ее гладкости (плавности) можно добиться лишь при многократной интуитивной корректировке проектировщиком вершин интерполяции.

Отсюда следует, что интерполяционные сплайны не являются математическим аппаратом оптимального трассирования, а лишь удобным и во многих задачах чрезвычайно эффективным инструментарием компьютерной обработки эскизно назначенных проектных решений. Качество таких решений существенно зависит от квалификации исполнителя.

Из вышеприведенных рассуждений вытекает, что постановка задачи трассирования на основе сплайнов должна предполагать следующее: вершины интерполяции эскизной трассы, а в случае реконструкции - исходной трассы, назначают приближенно (с допуском) и точное их местоположение вычисляют по определенным закономерностям, учитывающим ряд основополагающих целевых установок самого процесса трассирования. С использованием математической терминологии эту задачу можно отнести к задачам генерации геометрических форм по их грубым (приближенным) описаниям.

В качестве математического аппарата для решения задачи трассирования дорог рассмотрим сглаживающие сплайны, которые минимизируют функционал И. Шенберга:

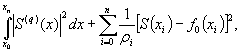
при ограничениях, например

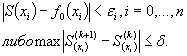
В записи функционала q = 1,2; S(x) - сплайн; r_i - весовой коэффициент узла интерполяции; f₀(x_i) - функция начального приближения.

Ограничения могут быть самыми разными и в случае трассирования дорог это: ограничения по допустимому радиусу, направлению трассы в плане и уклону в продольном профиле и т.д. При этом для сплайнов третьей степени (q = 2) должны быть добавлены так называемые «краевые условия» в точках х₀ = а, х_n = b, обеспечивающие единственность построения сплайна. Например, это могут быть условия заданного начального и конечного направления проектируемого участка трассы S'(x_а), S'(x_b).

Вышеприведенный функционал хорошо моделирует задачу трассирования дорог при их реконструкции, которая состоит в том, чтобы добиться минимального отклонения проектируемой трассы от существующей, при одновременных условиях по уклону и кривизне в продольном профиле и по кривизне и скорости нарастания кривизны в плане согласно требованиям СНиП для данной категории дороги. Минимальное отклонение достигается за счет второго слагаемого функционала, а условия по кривизне - за счет первого слагаемого.

Так как в процессе проектирования разбивку трассы ведут в виде пикетов, то удобнее выражать переменные координаты X, Y вершин этой трассы при помощи одного параметра l - текущей длины трассы. В этом случае на любом интервале трасса дороги в плане описывается единственным сочетанием элементов: сплайн-сплайн. Значение параметра l задает координатный вектор точки на трассе. В частности, для плана координаты точки на трассе математически описываются совокупностью параметрических сплайнов:

x = X_s(l),

y = Y_s(l).

Вычисление сглаживающих сплайнов 1-й и 3-й степени осуществляют, как правило, методом покоординатного спуска. Аналогичные результаты могут быть получены и при реализации метода штрафных функций.

Выше, в рассуждениях о Безье-кривых и сплайнах, понималось плоское расположение опорных точек трассы и, соответственно, рассматривалось представление только плоских кривых. В общем случае, трехмерное (рис. 28.9) векторное представление точек на трассе сплайнами относительно осей X, Y и Z имеет вид:

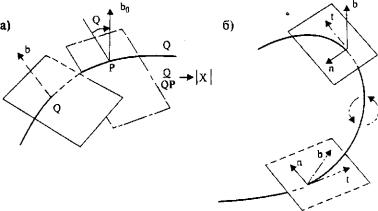
Рис. 28.9. Пространственное (трехмерное) проектирование оптимальной трассы автомобильных дорог:
а - вращение вокруг бинормали; б - вращение вокруг касательной (t)

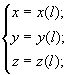
Если форма плоской кривой определяется функцией ее кривизны, то форма пространственной кривой однозначно определяется совокупностью двух функций: кривизны и кручения. Кривизна (r) и радиус кривизны (R = 1/r) пространственной кривой имеют тот же геометрический смысл, что и для плоской кривой, но вычисляется, естественно, по более сложной зависимости:

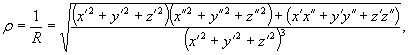где

x', x" - первая, вторая производные х по l и т.д.

Кручение - новое геометрическое понятие для трассы автомобильной дороги как кривой в пространстве, но именно кручением кривой можно объяснить многие из явлений зрительного восприятия, которые до сих пор оценивали и объясняли на основе лишь эмпирических правил. Кручение (Т) пространственной кривой в точке N следует определять по формуле:

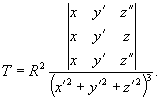
Геометрически кручение можно определить следующим образом: если Q - близкая к N точка кривой С, а q - угол между соприкасающимися плоскостями кривой С в точках N и Q, то при стремлении точки Q к точке N отношение угла q к расстоянию между Q и N стремится к определенному пределу, который и равен абсолютному кручению кривой С в точке N.

Для большего понимания геометрической сущности кручения приведем и ее кинематическое толкование. Представим себе, что некоторая плоскость перемешается в пространстве, причем ее фиксированная точка с единичной скоростью движется по кривой, фиксированная прямая в каждый момент времени касается кривой в этой точке, а сама плоскость все время является соприкасающейся плоскостью кривой. Тогда такое перемещение будет результатом поступательного движения и двух вращений - вращение этой плоскости вокруг бинормали (b) и ее вращение вокруг касательной (t). Угловая скорость первого вращения равна кривизне кривой, а второго - абсолютному кручению кривой в точке соприкосновения. Знак кручения связан с направлением вращения: в случае, когда вращение происходит против часовой стрелки, если смотреть из конца касательного вектора, то это плюс, а если по часовой стрелке - то минус.

Если при раздельном трассировании необходимо контролировать графики кривизны трассы раздельно в плане и продольном профиле, то при пространственном трассировании контроль должен осуществляться графиками пространственной кривизны и кручения.

Пространственное трассирование дорог можно также выполнять и на основе тангенциального хода с вписанными закруглениями в виде кривых Безье. Опорные точки характеристической ломаной Безье (тангенциального хода), в общем случае, задаются точками трехмерного пространства Р_i(х_i, y_i, z_i), i = 0,1, ...,т. Тогда пространственную кривую Безье степени m определяют уравнением:

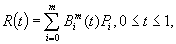где

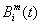- многочлены Бернштейна.

Матричная запись параметрических уравнений, описывающих пространственную кривую Безье:

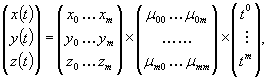где

0 # t # 1,

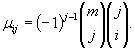
В случае, если промежуток изменения параметра произволен, а # t # b, уравнение кривой Безье имеет следующий вид:

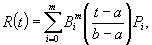
Полученным представлением пользуются при задании единой параметризации составной кривой Безье как целого:

R = R(t), t₀ # t # t_c , где

R = R⁽ⁱ⁾(t), t_i-1 # t # t_i, I = 1, 2,... l, - параметрическое векторное уравнение i-й элементарной кривой Безье.

Таким образом, как параметрические сплайны, так и кривые Безье позволяют осуществлять математически корректную запись трассы автомобильной дороги в пространстве. Это обстоятельство позволяет ставить и решать вопрос о методах пространственного трассирования дорог посредством сплайнов и кривых Безье.