Методы «однозначно определенной оси»

Методы «однозначно определенной оси» реализуют, как правило, на основе принципа «тангенциального трассирования». Феномен широкой применимости этого принципа можно объяснить тем, что для проектировщиков этот принцип привычен и потому более понятен, методы на его основе просты в расчетах и обеспечивают предельную экономичность полевого этапа работ.

Рассматривая детально этот принцип трассирования, можно заметить, что при «тангенциальном трассировании» трасса характеризуется ломаной линией, в изломы которой вписаны кривые. Отрезки прямых представляют собой касательные к кривым, поэтому можно говорить о ломаной как о тангенциальном ходе (полигоне). Полевое трассирование состоит, при этом, в последовательном вешении прямых линий тангенциального хода, отыскании и закреплении его вершин, измерениях углов поворота и расчетах пикетажного положения главных точек трассы (НК - начало кривой, КК - конец кривой, СК - середина кривой и т.д.) при заданных значениях радиусов закруглений. Рациональным в таком подходе является то, что ошибки, возможные при вписывании тех или иных кривых, не оказывают влияния на достоверность расчетов последующих кривых.

С принципом «тангенциального трассирования» практически однозначно связано то обязательное условие, что геодезические изыскания выполняют по «пикетному методу». Его суть заключается в следующем: при измерении линий теодолитного хода с помощью мерной ленты на этой линии закрепляют, как правило, пикеты (стометровые отрезки) и характерные точки трассы (водоразделы, лога, пересечения с автомобильными дорогами и инженерными коммуникациями и т.д.) и главные точки трассы. На каждом последующем отрезке ломаной пикетажное положение точек трассы устанавливают с учетом величины домера для каждой вписанной кривой в соответствующий угол поворота трассы. Далее перпендикулярно закрепленным точкам осуществляют съемку поперечных профилей на ширину полосы отвода. Таким образом, тангенциальный ход предопределяет очертания трассы и является основой для всех последующих геодезических работ. Естественно, что изменение или корректировка этой основы на этапе камеральных работ практически невозможна.

Отдельного рассмотрения требует процедура вписывания кривых в изломы тангенциального хода. Случай, когда закругления представляют собой круговые кривые, является простейшим и его применяют для дорог II-V категорий при R > 2000 м и при R > 3000 м - для дорог I-й категории. Для расчета такого закругления при известном угле поворота (q) и радиусе кривой (R) необходимо вычислить значения тангенса (Т), домера (Д), длины кривой (К) и биссектрисы (Б) (см. разд. 8.1). Когда закругления представлены круговыми кривыми с переходными кривыми, расчет не так однозначен, как в первом случае. При равной длине входной и выходной переходной кривой закругление является симметричным и необходимо рассчитывать те же элементы закругления, что и в первом случае. Если длины входной и выходной переходных кривых не равны между собой, то это случай несимметричного закругления. При его расчете уже отсутствует понятие биссектрисы закругления, что усложняет процесс закрепления и последующей разбивки такого закругления (см. разд. 9.2). В частном случае, если отсутствует круговая вставка между переходными кривыми, то такое закругление называют биклотоидой (симметричной или несимметричной, соответственно).

Случаи коробовой клотоиды и комбинированного закругления являются универсальными и служат для подбора любых очертаний закругления (см. главу 9). Расчет таких закруглений представляет собой достаточно сложную аналитическую задачу. Основы решения для составных закруглений известны, однако на практике реализация этих решений является задачей крайне непростой.

Закругления в виде классического сочетания геометрических элементов «клотоида - круговая кривая - клотоида» наиболее распространены в практике дорожного проектирования, но находят применение и другие типы закруглений (геометрических элементов). Например: кадиоиды 1-го и 2-го типов (проф. А.А. Белятынский), гиперболы и поликлотоиды (канд. техн. наук Ю.А. Фортуна), кубические параболы (канд. техн. наук В.А. Федотов), кривые Безье (д-р техн. наук В.Н. Бойков). Применение этих элементов обосновано соответствующими численными и натурными экспериментами и результатами сравнительного анализа.

Наиболее перспективными геометрическими элементами для проектирования закруглений трассы в составе тангенциального хода являются кривые Безье, которые способны принимать формы и свойства всех вышеприведенных элементов. К тому же кривые Безье являются в общем случае пространственными функциями и способны, как будет показано далее, обеспечивать пространственное (трехмерное) трассирование автомобильных дорог в едином классе функций.

В 1970 году П. Безье (французский математик) подобрал составляющие параметрического кубического многочлена таким образом, что их физический смысл стал очень наглядным и весьма подходящим для целей проектирования дорог по принципу «тангенциального трассирования».

Формула Безье для кубического многочлена (n = 3) имеет следующий вид:

Пусть 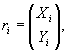i = 0, 1, 2, 3 - тогда для 0 # t # 1

r(t) = r₀(1 - t)³ + 3r₁t(1 - t)² + 3r₂t²(1 - t) + r₃t³

или в матричной форме:

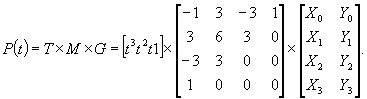
Матрицу М называют базисной матрицей кубической кривой Безье.

Помимо кривой Безье 3-го порядка (кубической) для целей трассирования дорог возможно применение также кривых Безье 2-го, 4-го и 5-го порядков. Соответствующие формулы для вычисления радиусов-векторов (и их производных) для этих кривых приведены ниже.

Кривая Безье 2-го порядка:

r(t) = r₀(1 - t)² + 2r₁t(1 - t) + r₂t².

Кривая Безье 4-го порядка:

r(t) = r₀(1 - t)⁴ + 4r₁t(1 - t)³ + 6r₂t²(1 - t)² + 4r₃t³(1 - t) + r₄t⁴.

Кривая Безье 5-го порядка:

r(t) = r₀(1 - t)⁵ + 5r₁t(1 - t)⁴ + 10r₂t²(1 - t)³ + 10r₃t³(1 - t)² + 5r₄t⁴(1 - t) + r₅t⁵.

Кривые Безье, обладающие особыми свойствами, как отмечалось выше, позволяют применять их в качестве универсальных кривых для проектирования закруглений трасс автомобильных дорог. В частности, построение кривой Безье опирается на характеристическую ломаную, которая и предопределяет ее свойства, некоторые их которых приведены ниже:

кривая Безье является гладкой кривой;

касательные в начале и конце кривой совпадают по направлению с первым и последним отрезками ломаной;

кривая Безье лежит в выпуклой оболочке, порожденной массивом точек (опорных вершин) ломаной;

кривая симметрична - сохраняет свою форму при перемене порядка вершин ломаной;

в случае, если вершины ломаной лежат в одной плоскости, то кривая Безье лежит в этой же плоскости;

степень функциональных коэффициентов кривой на единицу меньше количества вершин ломаной;

изменение положения хотя бы одной из вершин ломаной ведет к изменению очертаний кривой Безье.

Поскольку характеристическая ломаная и кривая Безье ассоциативно и функционально находятся в той же взаимозависимости, что и тангенциальный ход с трассой автомобильной дороги, то весьма привлекательно построение кривой Безье интерпретировать в терминах принципа "тангенциального трассирования".

На рис. 28.1,а представлена расчетная схема традиционного закругления «клотоида - круговая кривая - клотоида», вписанного в излом тангенциального хода с вершиной в точке Т и углом поворота q. Расстояние от начала кривой до вершины - тангенс Т₁. Расстояние от вершины до конца кривой - тангенс Т₂. Тангенсы Т₁ и Т₂ представляют собой касательные в начале и конце составного закругления, пересечение которых в точке Т и порождает характеристическую ломаную ATF. Если провести касательные в узлах стыковки элементов (точки N, М), то получим вспомогательную ломаную ANTMF.

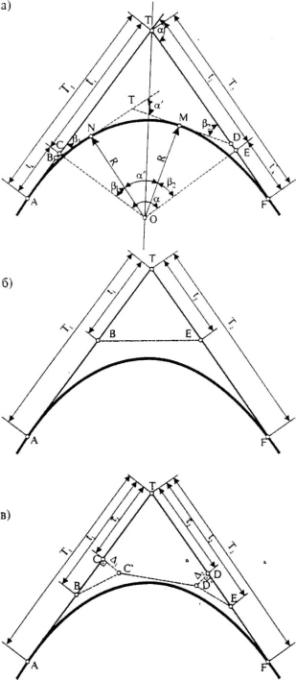
Рис. 28.1. Расчетные схемы закруглений трассы в плане
а - традиционная; б - Безье-3; в - Безье-5

Предположим, что в угол поворота q, образованный сторонами тангенциального хода, требуется вписать закругление трассы посредством кривой Безье 3-й степени (Безье-3). Поставим (см. рис. 28.1, б) начальную А и конечную F точки кривой соответственно на 1-й и 2-й сторонах тангенциального хода. Внутренние точки (В, Е) характеристического многоугольника разместим в вершине утла. Расстояния от заданных точек до вершины будем называть, следуя сложившейся дорожной терминологии, большими тангенсами (Т₁ и Т₂). По трем заданным точкам будет построена кубическая кривая Безье со сдвоенной вершиной в точке Т. Если полученные очертания кривой по каким-либо соображениям не устраивают инженера-проектировщика, то варьировать очертаниями кривой можно за счет изменения положения точек В и Е. При этом точки будут перемещаться вдоль соответствующих сторон тангенциального хода. Расстояния от вершины до этих точек условимся называть малыми тангенсами кривой (t₁, t₂). Таким образом, варьируя значениями малых и больших тангенсов, можно получать кривые разного очертания и разных дифференциальных свойств. В частности, как будет показано ниже, кривая Безье-3 может с успехом моделировать прямую, дугу окружности, клотоиду и отрезок клотоиды.

Недостатком Безье-3 является то, что при моделировании закругления единой кривой в средней части закругления невозможно добиться участка постоянной кривизны.

Чтобы получить фрагмент дуги окружности в средней части закругления, следует обратиться к кривой Безье 5-й степени (Безье-5), характеристическая ломаная которой состоит из 6-и точек. На рис. 28.1,в эта ломаная образована точками А, В, С, D, Е, F. В терминах тангенциального хода построение Безье-5 выглядит следующим образом. Начальная точка А находится на расстоянии Т₁ от вершины, точка В - на расстоянии t₁. Касательная в начале Безье-5 будет совпадать с направлением АВ. Положение третьей точки С условимся отмерять также от вершины Т тангенсом т,, Но если точки А и В могут перемещаться лишь вдоль стороны тангенциального хода, тем самым задавая направление касательной в начале кривой, то точка С может смещаться на Д, влево и вправо от стороны тангенциального хода, формируя разнообразные очертания гладких кривых. Расположение точек D, Е, F на 2-й стороне тангенциального хода сходно расположению точек А, В, С и, поэтому, не требует дополнительных пояснений.

Единой кривой Безье-5 можно также моделировать серпантины 1-го и 2-го рода, левосторонние и правосторонние соединительные рампы на пересечениях в разных уровнях.