Лучистый теплообмен между газовой средой и оболочкой.
 Предположим, что газ имеет постоянную температуру ТГ, а стенка ТС. Примем, что газ и стенка являются серыми телами. Излучение стенки (оболочки) характеризуется сплошным спектром. Газовая среда имеет селективно-серое излучение в виде отдельных полос e1g1;e2g2(рис. 18.8). В общем случае число таких полос для различных газов может быть различным.
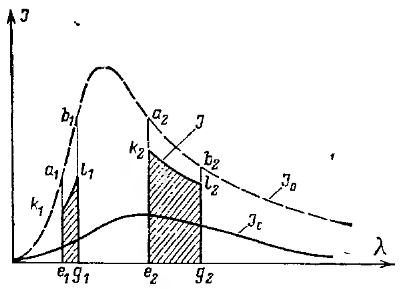
Предположим, что газ имеет постоянную температуру ТГ, а стенка ТС. Примем, что газ и стенка являются серыми телами. Излучение стенки (оболочки) характеризуется сплошным спектром. Газовая среда имеет селективно-серое излучение в виде отдельных полос e1g1;e2g2(рис. 18.8). В общем случае число таких полос для различных газов может быть различным.
Рис 18.8. К лучистому теплообмену между селективно-серым газом и серой стенкой.
Газовая среда обменивается лучистыми потоками со стенкой только в пределах этих полос. Вне спектральных полос отдельные элементы стенки обмениваются лучистыми потоками только между собой.
Для изотермической стенки результирующий поток для этого теплообмена будет равен нулю. Тогда лучистый поток от газа к стенке можно выразить зависимостью
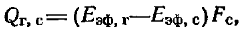 (18.39)
(18.39)
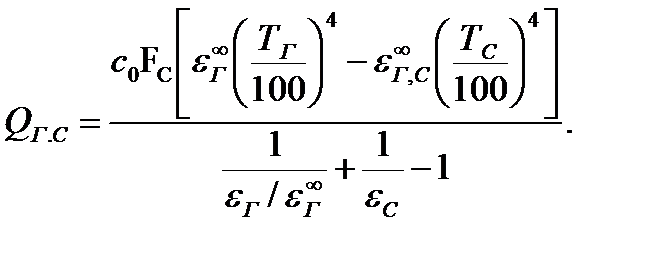 Расчетное уравнение для лучистого потока QГ,С Вт, передаваемого от газовой среды к стенке:
Расчетное уравнение для лучистого потока QГ,С Вт, передаваемого от газовой среды к стенке:
(18.40)
Интегральные значения степени черноты (коэффициента поглощения) для смеси газон, как указывалось выше, в общем случае не равны сумме значений их для отдельных компонентов смеси. Так, для смеси Н2О и СО2 степень черноты и коэффициент поглощения меньше суммы их значений для Н2О и СО2, что объясняется частичным совпадением их спектров излучения:
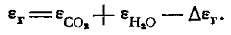 (18.41)
(18.41)
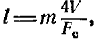 Степени черноты пара и двуокиси углерода берутся из графиков (18.4), (18.5) по температуре газа при соответствующих произведениях парциального давления на длину пути луча (pl). Приближенно средняя длина пути луча определяется из соотношения
Степени черноты пара и двуокиси углерода берутся из графиков (18.4), (18.5) по температуре газа при соответствующих произведениях парциального давления на длину пути луча (pl). Приближенно средняя длина пути луча определяется из соотношения
(18.42)
где V— объем газового тела; m = 0,9 — поправочный коэффициент.
Данные по средней длине пути луча для газовых тел различ-ной геометрической формы приводятся в литературе. Поправка на отклонение от закона аддитивности для газовых смесей за счет взаимного поглощения излучения компонен-тами берется изграфиков на рис. 18.7. Предельные степени черноты газа при ТГи ТСберутся из графика рис. 18.6.
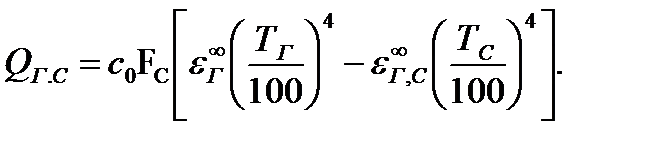 Если газ является селективно-черной средой, а стенка черной поверхностью, то расчетное уравнение упрощается:
Если газ является селективно-черной средой, а стенка черной поверхностью, то расчетное уравнение упрощается:
(18.43)
Рассмотренный метод расчета теплообмена излуче-нием относится к газовым средам, не содержащим взвешенных твердых частиц несгоревших продуктов сгорания. В камерах сгорания топок и печей газовые потоки содержат указанные твердые частицы. Для расчета лучистого теплообмена в топках и печах существуют различные методики, приведенные в специальной литературе.
Сложный теплообмен
Лучистый перенос может сопровождаться одновременным переносом тепла путем теплопроводности и конвекции. Совместный (комбинированный) процесс лучистого теплообмена и процесса теплопроводности или конвекции, а также всех трех видов переноса называют сложным теплообменом.
Среди процессов сложного теплообмена различают радиационно - конвективный и радиационно - кондуктивный теплообмен.
Радиационно-конвективный перенос теплоты является наиболее общим случаем сложного теплообмена; при этом теплота переносится не только радиацией, но и теплопроводностью, и конвекцией. В радиационно-кондуктивном теплообмене имеет место перенос теплоты в неподвижной ослабляющей и тепло-проводной среде путем излучения и теплопроводности.
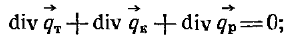 Сложный теплообмен описывается системой уравнений, состоящей из уравнений энергии, движения и сплошности, к которым добавляются условия однозначности. Для модели сплошной среды уравнения сохранения массы и количества движения остаются неизменными. Уравнение энергии применительно к радиационно-конвективному стационарному теплообмену в однокомпонентной несжимаемой жидкости, поглощающей, испускающей и рассеивающей энергию излучения, будет иметь вид:18.44)
Сложный теплообмен описывается системой уравнений, состоящей из уравнений энергии, движения и сплошности, к которым добавляются условия однозначности. Для модели сплошной среды уравнения сохранения массы и количества движения остаются неизменными. Уравнение энергии применительно к радиационно-конвективному стационарному теплообмену в однокомпонентной несжимаемой жидкости, поглощающей, испускающей и рассеивающей энергию излучения, будет иметь вид:18.44)
здесь qТ, qКи qР — соответственно векторы плотности теплового потока за счет теплопроводности, конвекции и излучения (радиации).
В общем случае эти величины изменяются в рассматриваемом про-странстве. В уравнении (18.44) не учитываются возможные внутрен-ние источники теплоты и диссипация механической энергии.
Граничные условия задаются различно в зависимости от постановки задачи. Различным образом могут быть заданы физические и оптичес-кие параметры среды и граничной поверхности.
Задачи о совместном переносе энергии путем теплопро-водности и излучения вобщем случае являются весьма сложными, поэтому они решаются численными или при-ближенными методами. Однако применительно к оптичес-ки тонким и оптически толстым слоям эти задачи имеют простые решения. При отсутствии конвекции зависимость (18-44) с учетом того, что согласно закону Фурье qТ = — lgrad t, принимает вид: div(lgrad t) = div qР
Для одномерной и плоской задачи это соотношение переходит в зависимость
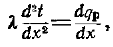
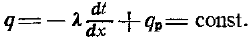 что эквивалентно равенству
что эквивалентно равенству
(18.45)
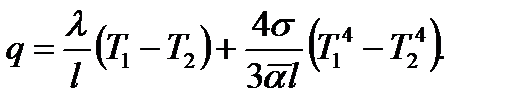 В случае оптически толстого слоя среды :
В случае оптически толстого слоя среды :
(18.47)
Уравнение (18.47) показывает, что и в случае оптически толстого слоя среды потоки qТ и qР не зависят друг от друга, общий поток определяется их суммой. Задачи радиационно-конвективного теплообмена даже для простых случаев обычно более трудны, чем задача радиационно-кондуктивного теплообмена.
Дата добавления: 2021-06-28; просмотров: 755;











