Уравнения переноса энергии в поглощающей среде

Существуют полупрозрачные среды, обладающие конечным пропусканием лучистой энергии (полупроводники, керамика, стекло, газы, пары и др.). Кроме того, среда может иметь собственное излучение. Вследствие этого интенсивность излучения вдоль какого-либо направлении (l) будет изменяться. Уравнение, определяющее изменение интенсивности луча за счет поглощения, излучения и рассеивания среды, называется уравнением переноса лучистой энергии.

Интенсивность излучения по отдельным длинам волн при прохождении в направлении l через слой поглощающей среды толщиной dlумень-шается пропорционально этой интенсивности и бесконечно малому пути луча dl:

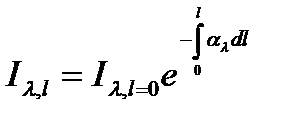Зависимость позволяет найти спектральную яркость излучения в каждой точке направления l для отдельных длин волн.

Поглощательная способность среды для данной длины волны определяется по отношению лучистой энергии, поглощенной в слое толщиной l к энергии, падающей на границу этого слоя:

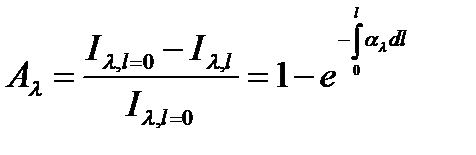Введем оптическую толщину среды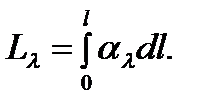

Если спектральный коэффициент поглощения является постоянной величиной по длине луча, то оптическая толщина среды будет равна:

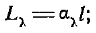
здесь l —полная толщина слоя среды.
Тогда зависимость, выражающая ослабление интенсивности излучения в поглощающей среде, принимает вид: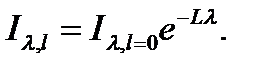

Уравнение (18.6) носит название закона Бугера.
Поглощательиая способность среды в этом случае представится вместо соотношением

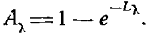
Уравнение переноса энергии в поглощающей и излучающей среде
При прохождении тепловых лучей в поглощающей среде погло-щенная энергия переходит в теплоту и снова излучается средой. Выше принималось, что среда, поглощая лучистую энергию, заметно ее не перизлучает. В более общем случае интенсивность среды вдоль луча будет уменьшаться вследствие поглощения, но и увеличиваться за счет собственного излучения. Тогда вместо зависимости уравнение переноса принимает вид:

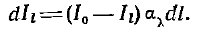
Этузависимость можно получить из теплового баланса. Лучистая энергия, поглощенная средой в слое толщиной dl, как и ранее, определяется величиной .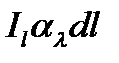

Интенсивность собственного излучения можно выразить через интенсивность абсолютно черного тела и коэффициент поглощения a_lвеличиной .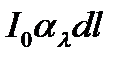

Зависимости можно придать другой вид, учитывая, что согласно закону Кирхгофа для поглощающей среды :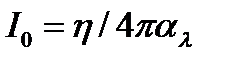

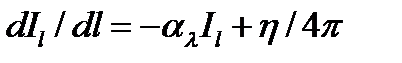
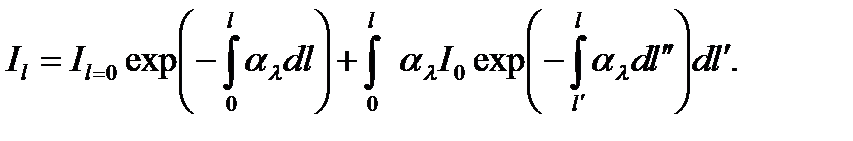
Первое слагаемое определяет долю интенсивности падающего из-лучения I_l = 0, проходящего путь от 0 до l; второе — интенсивность собственного излучения, возникающего на всем протяжении элемен-тов среды длиной dl¢ и переданного от l¢до l, где 0 £ dl¢£l лежит на отрезке l — l¢.

В целом зависимость (18.11) выражает интенсивность излучения как функцию координат точки, направления lи длины волны в поглощающей и излучающей среде.
В частном случае постоянных величин температуры, оптических свойств среды и давления (для газов) уравнение принимает вид:

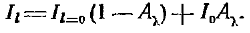
Интенсивность излучения, поступающего в среду на границе l = 0, определяется свойствами поверхности (стенки), ограничивающей поглощающую среду. Для диффузной стенки (при D = 0)

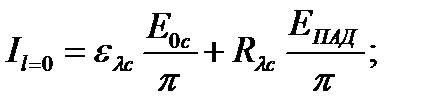
здесь e_lC и R_lC— спектральные степень черноты и отражательная способность стенки; I_0C = E_ПАД/p — спектральная интенсивность излучения абсолютно черного тела при температуре стенки; I_ПАД = E_ПАД/p — то же для потока излучения, падающего на стенку.

Для серой стенки e_lC и R_lCне зависят от длины волны.
Подставляя (18.14) в зависимость (18.13) и проведя интегрирование по спектру, получаем:

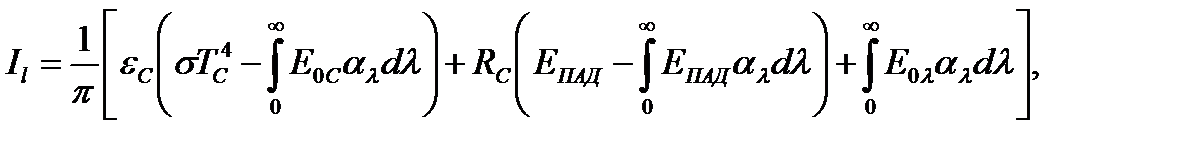
где Е_0l, Е₀— плотности потоков спектрального и интегрального излучения абсолютно черного тела при температуре среды Т.
Последнее уравнение позволяет найти средние интегральные значения для поглощательной способности и степени черноты среды:

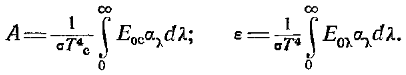
В интеграле величина E_ПАД состоит из энергии, излученной средой или другими стенками и прошедшей через среду.