Тепловой расчет теплообменных аппаратов. Виды теплообменных аппаратов. Ур-иетепл баланса. Основные положения. Ур-ие теплопередачи.


КЛАССИФИКАЦИЯ ТЕПЛООБМЕННЫХ АППАРАТОВ Теплообменники — это устройства, в которых теплота переходит от одной среды к другой.теплоты в них происходит конвекцией, теплопроводностью; а если хоть один из теплоносителей газ, то и излучением. Теплообмен между теплоносителями является одним из наиболее важных и часто используемых в технике процессов. Выделяются еще теплообменные устройства, в которых нагрев или охлаждение теплоносителя осуществляется за счет внутренних источников тепла. Рекуперативные теплообменные аппараты- устройства, в которых две жидкости с различными температурами текут в пространстве, разделенном твердой стенкой. Теплообмен =>за счет конвекции и теплопроводности стенки, а если хоть одна из жидкостей является излучающим газом, то и за счет теплового излучения. Примеры - парогенераторы, подогреватели, конденсаторы, выпарные аппараты и др. Рекуператоры работают, как правило, в стационарном тепловом режиме. Регенераторы — такие ТА, в которых одна и та же поверхность нагрева через определенные промежутки времени омывается то горячей, то холодной жидкостью. Сначала по­верхность регенератора отбирает теплоту от горячей жидкости и нагревается, затем поверхность регенератора отдает энергию холодной жидкости. В регенераторах теплообмен всегда происходит в нестационарных условиях, тогда как рекуперативные теплообменные аппараты большей частью работают в стационарном режиме. Так как в регенеративных и рекуперативных аппаратах процесс передачи теплоты неизбежно связан с поверхностью твердого тела, то их еще называют поверхностными.В смесительных аппаратах теплопередача осуществляется при непосредственном контакте и смешении горячей и холодной жидкостей. Примером = градирни тепловых электрических станций. В градирнях вода охлаждается атмосферным воздухом. Воздух непосредственно соприкасается с водой и перемешивается с паром, возникающим из-за частичного испарения воды. В этом процессе объединяются тепло- и массообмен.В теплообменниках с внутренними источниками энергии применяются не два, как обычно, а один теплоноситель, который отводит теплоту, выделенную в самом аппарате. Примером = ядерные реакторы, электронагреватели и другие устройства. С теплотехнической точки зрения все аппараты имеют одно назначение — передачу теплоты от одного теплоносителя к другому или поверхности твердого тела к движущимся теп­лоносителям. Последнее и определяет те общие положения, которые лежат в основе теплового расчета любого теплообменного аппарата.ОСНОВНЫЕ ПОЛОЖЕНИЯ И УРАВНЕНИЯ ТЕПЛОВОГО РАСЧЕТА Тепловые расчеты теплообменных аппаратов могут быть проектными и поверочными.Проектные (конструктивные) тепловые расчетывыполняются при проектировании новых аппаратов, целью расчета является определение поверхности теплообмена.

Поверочные тепловые расчеты выполняются в случае, если известна поверхность нагрева теплообменного аппарата и требуется определить количество переданного тепла и конечные температуры рабочих жидкостей. Тепловой расчет теплообменных аппаратов сводится ксовместному решению уравнений теплового баланса и теплопередачиУравнения теплового баланса и теплопередачи, будучи едиными по существу, различны в деталях в зависимости от типа рассматриваемого теплообменника (рекуперативный, регенеративный или смесительный). РЕКУПЕРАТИВНЫЕ АППАРАТЫ1. Основные положения теплового расчета. Тепловой расчет теплообменного аппарата может быть конструкторским, целью которого является определение площади поверхности теплообмена, и поверочным, при котором устанавливается режим работы аппарата и определяются конечные температуры теплоносителей. В обоих случаях (проектном и поверочном) основными расчетными уравнениями являются:уравнение теплопередачи Q= kF(t1 — t2) (1)и уравнение теплового балансаQ1= Q2+ DQ, гдеQ1 = G1di1= G1cp1dt1= G1cp1(t¢1—t¢¢1)(2)—количество теплоты, отданное горячим теплоносителем; Q2 = G2di2= G2cp2dt2= G2cp2(t¢¢2— t¢2)— количество теплоты, воспринятое холодным теплоносителем; DQ — потери теплоты в окружающую среду; G1, G2— массовые расходы горячего и холодного теплоносителей; dt1, dt2— изменение энтальпии теплоносителей; cp1,cp2— удельные теплоемкости теплоносителей при постоянном давлении; t¢1,t¢¢1— температуры горячего теплоносителя на входе и выходе из аппарата; t¢2— t¢¢2— температуры холодного теплоносителя на входе и выходе его из аппарата. Однако это положение для всей поверхности справедливо приближенно лишь при кипении жидкости и конденсации паров. В общем случае температура рабочих жидкостей в теплообменниках изменяется: горячая охлаждается, а холодная нагревается. Вместе с этим изменяется и температурный напор между ними Dti = (t1—t2)i. В таких условиях уравнение теплопередачи (1) применимо лишь в дифференциальной форме к элементу поверхности dF, а именно: 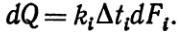Общее количество теплоты, переданное через всю пов-ерхность, определяется интегралом этого выражения 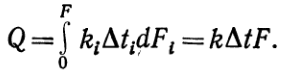(3)Это и есть расчетное уравнение теплопередачи. Здесь Dt— среднее значение температурного напора по всей поверхности нагрева.В тепловых расчетах важное значение имеет величина, называемая водяным эквивалентом, W, Дж/(с×K), Вт/K: 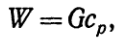(4)где G = rwf— массовый расход теплоносителя; w— скорость теплоносителя; r — плотность теплоносителя; f — площадь сечения канала.Если величину Wввести в уравнение теплового баланса (2), то оно принимает вид: 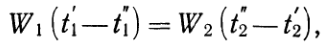откуда 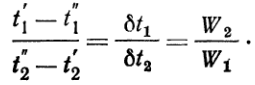(5) = отношение изменений температур рабочих жидкостей обратно пропорционально отношению их водяных эквивалентов. Такое соотношение справедливо как для всей поверхности нагрева F, так и для каждого ее 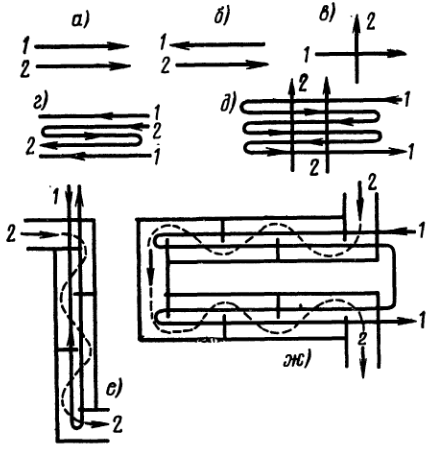элемента dF, т. е. 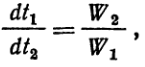где dt1и dt2— изменения температуры рабочих жидкостей на элементе поверхности.Характер изменения температуры рабочих жидкостей вдоль поверхности нагрева зависит от схемы их движения и соотношения величин W1и W2. Если в теплообменном аппарате горячая и холодная жидкости протекают параллельно и в одном направлении, то такая схема движения называется прямотоком(рис.1, а).Если жидкости протекают параллельно, но в прямо противоположном направлении,— противотоком (рис.1, б). Если жидкости протекают в перекрестном направлении,— перекрестным током(рис.1, в). Помимо таких простых схем движения, на практике осуществляются и сложные: одновременно прямоток и противоток (рис.1, г), многократно перекрестный ток, (рис.1, д—ж) и т.дВ зависимости от того, осуществляется ли прямоток или противоток и W1больше или меньше, чем W2, получаются четыре характерные пары кривых изменения температуры вдоль поверхности нагрева, представленные на рис.2. Здесь по осям абсцисс отложена площадь поверхности нагрева F, а по осям ординат — температура рабочих жидкостей. В соответствии с уравнением (5) на графиках большее изменение температуры t' — t" = dtполучается для той жидкости, у которой значение величины Wменьше.Из 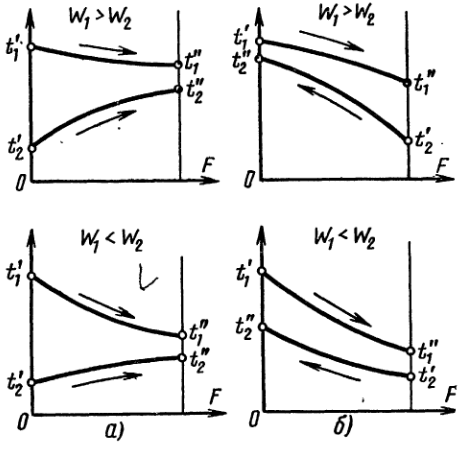рассмотрения графиков следует, что при прямотоке конечная температура холодной жидкости t¢¢2всегда ниже конечной температуры горячей жидкости t¢1. При противотоке же конечная температура холодной жидкости t¢¢2может быть выше конечной температуры горячей t¢1. Следовательно, при одной и той же начальной температуре холодной жидкости при противотоке ее можно нагреть до более высокой температуры, чем при прямотоке.Температурный напор вдоль поверхности при прямотоке изменяется сильнее, чем при противотоке. Среднее значение температурного напора при противотоке больше, чем при прямотоке. За счет этого при противотоке теплообменник получается компактнее. Если температура хотя бы одной из рабочих жидкостей постоянна, то среднее значение температурного напора независимо от схемы движения оказывается одним и тем же. Так именно получается при кипении жидкостей и при конденсации паров, либо когда расход одной рабочей жидкости настолько велик, что ее температура изменяется очень мало. Рассмотрев общие уравнения теплового расчета аппаратов и уяснив температурные условия работы теплообменников, перейдем теперь к более подробному рассмотрению величин.

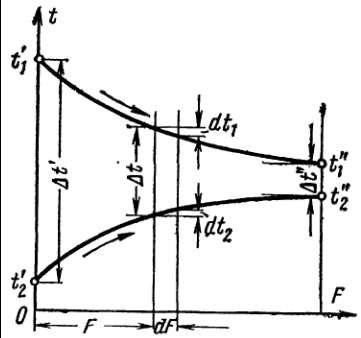57. Средний температурный напор. Определение коэффициента теплопередачи при расчете теплообменных аппаратов. Расчет конечной температуры рабочих жидкостей.Средний температурный напор. При выводе формулы осреднения температурного напора рассмотрим простейший теплообменный аппарат, работающий по схеме прямотока. Количество теплоты, передаваемое в единицу времени от горячей жидкости к холодной через элемент поверхности dF(рис.3), определяется уравнением
(а)
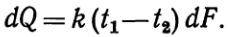(а)

При этом температура горячей жидкости понизится на dt1, а холодной повысится наdt2.Следовательно,

 

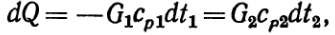(б)

откуда 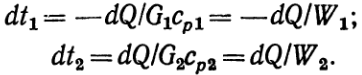(в) (г)

Изменение температурного напора при этом

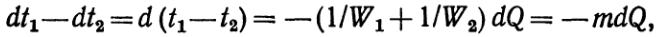(д)где т = 1/W1+ 1/W2Подставляя в уравнение (д) значение dQиз уравнения (а), получаем:

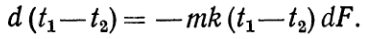(е) Обозначим (t1— t2) через Dt и произведем разделение переменных: 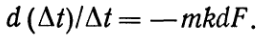(ж) Если значения ти kпостоянны, то, интегрируя уравнение (ж) получаем: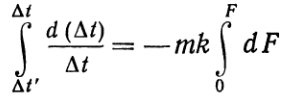

или 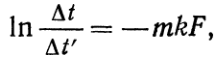(з)откуда 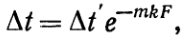(и)где Dt— местное значение температурного напора (t1—t2), относящееся к элементу поверхности теплообмена.Из уравнения (и) видно, что вдоль поверхности нагрева температурный напор изменяется по экспоненциальному закону. Зная этот закон, легко установить и среднее значение температурного напора 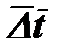. На основании теоремы о среднем (при k= const) имеем: 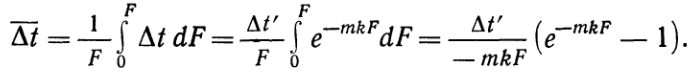(к)Подставляя в уравнение (к) значение mkFи 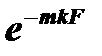из уравнений (з) и (и) и имея в виду, что согласно рис.3 в конце поверхности нагрева Dt=Dt¢¢, окончательно имеем: 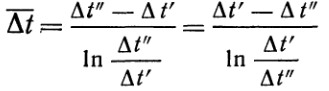и 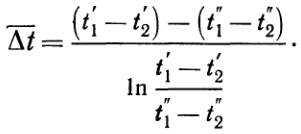Такое значение температурного напора называется среднелогарифминескими часто в литературе обозначается DtЛОГ.Точно таким же образом выводится формула осреднения температурного напора и для противотока. Отличие лишь в том, что в правой части уравнения (г) следует поставить знак минус, и поэтому здесь т = 1/W1 — 1/W2. Окончательная формула для среднего логарифмического температурного напора при противотоке имеет вид: 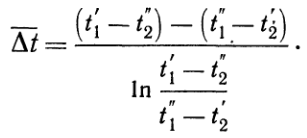При равенстве величин W1и W2в случае противотока (т = 0) из уравнения (и) имеем: Dt= Dt'. В этом случае температурный напор по всей поверхности постоянен: 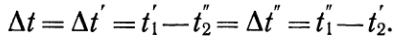(8)Формулы (7) и (8) можно свести в одну, если независимо от начала и конца поверхности через Dtб обозначить больший, а через DtМ меньший температурные напоры между рабочими жидкостями. Тогда окончательная формула среднелогарифмического температурного напора для прямотока и противотока принимает вид: 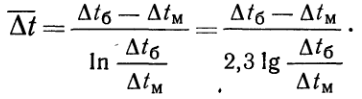(9)В тех случаях, когда температура рабочих жидкостей вдоль поверхности нагрева изменяется незначительно, средний температурный напор можно вычислить как среднеарифметическое из крайних напоров Dt'и Dt": 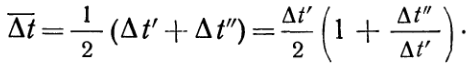(10)Среднеарифметическое значение температурного напора всегда больше среднелогарифмического. Но при Dt"/Dt'> 0,6 они отличаются друг от друга меньше чем на 3%. Такая погрешность в технических расчетах вполне допустима.Для аппаратов с перекрестным и смешанным током рабочих жидкостей задача об усреднении температурного напора отличается сложностью математических выкладок. Поэтому для наиболее часто встречающихся случаев результаты решения обычно представляются в виде графиков. Для ряда схем такие графики приведены в приложении. При помощи их расчет среднего температурного напора производится следующим образом. Сначала по формуле (8) определяется среднелогарифмический температурный напор как для чисто противоточных аппаратов. Затем вычисляются вспо­могательные величины Ри R:

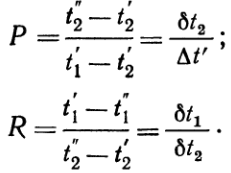(11) (12)

По этим данным из соответствующего вспомогательного графика находится поправка 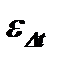. Итак, в общем случае средний температурный напор определяется формулой

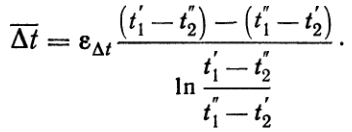(13)

 

 

Коэффициент теплопередачи. При расчете теплообменных аппаратов возникают трудности с определением значения коэффициента теплопередачи k. определяются изменением температуры рабочих жидкостей и сложностью геометрической конфигурации поверхности теплообмена. Практически определение значения коэффициента теплопередачи производится по характерным формулам. Специфические же особенности процесса теплообмена в рассчитываемых аппаратах учитываются при выборе значений коэффициентов теплоотдачи а, которые входят в формулу для коэффициента теплопередачи.При расчете kв первую очередь необходимо произвести анализ частных термических сопротивлений, и если возможно, то следует произвести упрощение расчетной формулы. Далее необходимо учитывать влияние на коэффициент теплопередачи изменения температуры рабочих жидкостей. Большей частью такой учет сводится к отнесению коэффициентов теплоотдачи к средним температурам рабочих жидкостей. Для жидкости с большим водяным эквивалентном средняя температура берется как среднеарифметическое из крайних значений, например, t6 = 0,5 (t¢6 + t¢¢6). При этом для другой жидкости, с меньшим водяным эквивалентом, средняя температура определяется из соотношения 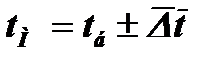. Здесь 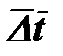является среднелогарифмическим температурным напором; знак «—» применяется в тех случаях, когда t6означает температуру горячей жидкости, а знак «+» в тех случаях, когда tб означает температуру холодной жидкости.Иногда вычисление коэффициента теплопередачи производят по температурам рабочих жидкостей в начале и в конце поверхности нагрева. Если полученные значения k'и k"друг от друга отличаются не очень сильно, то среднеарифметическое из них принимается за среднее значение k,а именно:

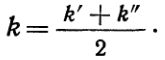(14)В большинстве практических случаев такое осреднение является достаточным. В случае же сильного расхождения между собой значений k'и k"необходимо разделить поверхность нагрева на отдельные участки, в пределах которых коэффициент теплопередачи изменяется незначительно, и для каждого такого участка расчет теплопередачи производить раздельно.Так же поступают и в тех случаях, когда резко меняются условия омывания поверхности нагрева рабочей жидкостью, например, в нижней части поверхности нагрева поперечноеомывание, в средней — продольное и в верхней — снова поперечное. Если при этом температура рабочей жидкости изменяется незначительно, то применяется осреднение: 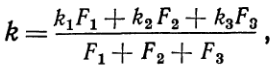(15)где F1,F2и F3— отдельные участки площади поверхности нагрева; k1,k2и k3— средние значения коэффициента теплопередачи на этих участках.

Расчет конечной температуры рабочих жидкостей. Выше конечной целью теплового расчета являлось определение площади поверхности нагрева и основных размеров теплообменника для его дальнейшего конструирования. Предположим теперь, что теплообменник уже имеется или по крайней мере спроектирован. В этом случае целью теплового расчета является определение конечных температур рабочих жидкостей. Это — так называемый поверочный расчет.

При решении такой задачи известными являются следующие величины: площадь поверхности нагрева F, коэффициент теплопередачи k,величины W1и W2и начальные температуры t¢1и t¢2, а искомыми: конечные температуры t¢¢1и t¢¢2и количество переданной теплоты Q.В приближенных расчетах можно исходить из следующих представлений. Количество теплоты, отдаваемое горячей жидкостью, равно:

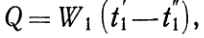(16)

откуда конечная температура ее t¢¢1определяется соотношением 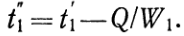(а)

Соответственно для холодной жидкости имеем: 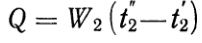(17)

и
(б)
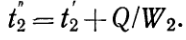(16)

Если принять, что температуры рабочих жидкостей меняются по линейному закону, то

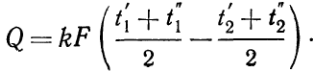(в)

Вместо неизвестных t¢¢1и t¢¢2подставим их значения из уравнения (а) и (б), тогда получим:

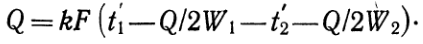(г)

Произведя дальнейшее преобразование, получим:

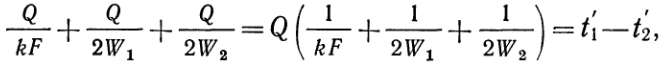(д)

откуда окончательно получаем: 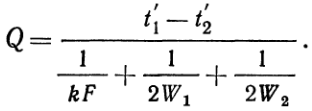(18)

Зная количество переданной теплоты Q, очень просто по формулам (а) и (б) определить и конечные температуры рабочих жидкостей t¢¢1и t¢¢2. Приведенная схема расчета хотя и проста, однако применима лишь для ориентировочных расчетов и в случае небольших изменений температур жидкостей. В общем же случае конечная температура зависит от схемы движения рабочих жидкостей. Поэтому для прямотока и противотока приводится вывод более точных формул.


 


Дата добавления: 2021-06-28; просмотров: 567;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.019 сек.