Природа гироскопического момента

Рассматривая основные свойства гироскопа, мы заметили одну несколько неожиданную особенность его поведения. При действии момента внешней силы гироскоп не поворачивается в том направлении, в котором этот момент стремится его повернуть, а прецессирует вокруг оси, перпендикулярной приложенному моменту. Это свидетельствует о том, что по неизвестным пока причинам в рассматриваемых условиях возникает некоторый момент, обусловленный реакцией гироскопа, который уравновешивает момент внешней силы. Очевидно, что этот момент, названный гироскопическим моментом, по модулю равен приложенному извне моменту и направлен в противоположную сторону. Определим силы, порождающие указанный момент.

С этой целью обратимся к рис. 2.12. Выберем в роторе некоторую i-ю точку с массой m_i, радиус – вектор ρ_i которой составляет с осью оу угол φ_i. За счет вращения ротора с угловыми скоростями ω_z и Ω на выбранную точку будут действовать центробежные силы f_1i и f_2i , соответственно. Однако вследствие того, что обе эти силы лежат в плоскости ротора и их плечи относительно осей оу и oz равны нулю, они не могут создать интересующий нас гироскопический момент. Единственной силой, которая может это сделать, является сила кориолиса f_3i (см. приложение П2). Величина указанной силы определяется следующим равенством:

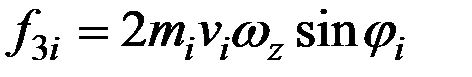, (2.7)

где v_i – линейная скорость выбранной нами точки.

Моменты М_уi и M_zi этой силы относительно осей, оу и oz, соответственно, будут равны:

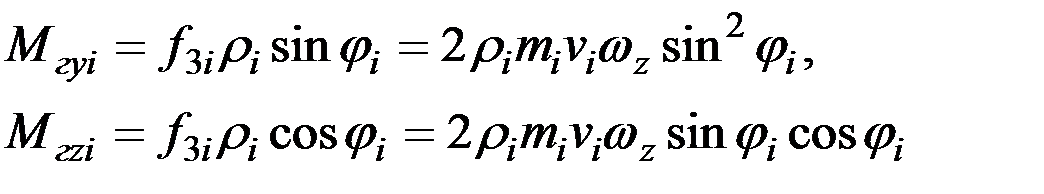(2.8)

Принимая во внимание, что произведение 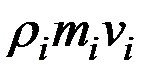представляет собой момент количества движения Н_i i – ой точки относительно оси ох, равенства (2.8) можно переписать в следующем виде:

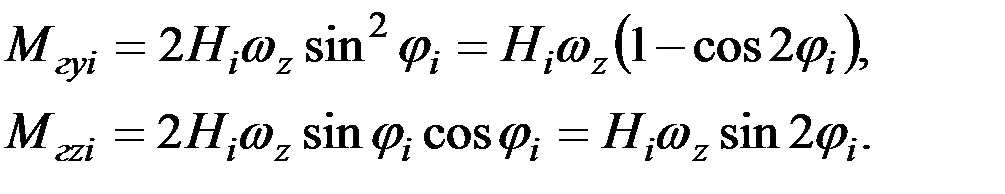(2.9)

Результирующий гироскопический момент, создаваемый всеми N материальными точками ротора вокруг оси оу, будет равен

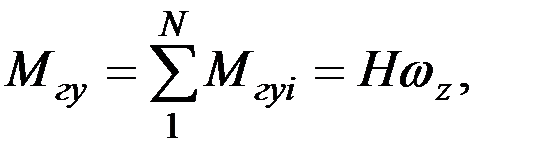(2.10)

где Н – результирующий кинетический момент ротора. В силу периодичности функций sin2φ_i и cos2φ_i результирующий момент M_гz и составляющая 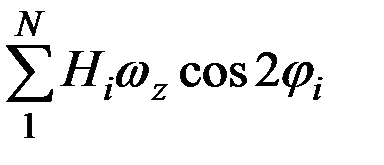,будут равны нулю.

В том случае, если момент внешней силы приложен к оси oz, прецессия гироскопа будет иметь место вокруг оси оу, и величина момента гироскопической реакции будет определяться следующим равенством:

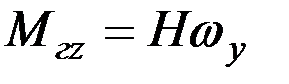. (2.11)

Важно!

Таким образом, при воздействии на гироскоп момента внешней силы в результате его прецессии возникают силы кориолиса, образующие момент гироскопической реакции, который уравновешивает приложенный извне момент. Величина момента гироскопической реакции равна произведению кинетического момента гироскопа на угловую скорость его прецессии. Вектор гироскопического момента направлен перпендикулярно векторам Н и угловой скорости прецессии в ту сторону, откуда с его конца движение по кратчайшей траектории вектора Н к вектору скорости прецессии видно происходящим против часовой стрелки.