Задачи, решаемые гироскопическими системами

В процессе судовождения возникает необходимость решения задач, связанных:

· с определением места судна и параметров движения его центра масс;

· с получением информации о пространственном положении судна и параметрах его качки;

· с автоматическим управлением движением судна.

Первые две задачи являются информационными, поскольку имеют своей целью обеспечение судоводителя или системы автоматического управления движением судна (авторулевого) данными, необходимыми для принятия соответствующих решений или формирования управляющего сигнала. Принципы построения и особенности работы систем, решающих именно эти задачи, будут рассмотрены в данной книге.

Третья задача в определенной степени является самостоятельной и охватывает вопросы, связанные с синтезом оптимального управления движением судна в различных условиях плавания.

Определение места судна можно производить двумя принципиально различными способами. Первый предусматривает измерение его положения относительно ориентиров, координаты которых известны, с последующим пересчетом результатов измерений в систему координат, в которой наблюдается движение судна. Такие пересчеты, как правило, не требуют операций интегрирования и не порождают ошибок, нарастающих во времени. Указанный способ используется в спутниковых и радионавигационных системах, при определении места судна путем пеленгования наземных ориентиров, при использовании для этих целей радиолокаторов и астрономических наблюдений.

Основной его недостаток обусловлен неавтономностью источников первичной информации и, как следствие, зависимостью полученных результатов от множества внешних факторов, таких как условия плавания, наличие видимости ориентиров, наличие помех, мешающих проведению необходимых измерений.

Второй способ основан на вычислении пути, пройденного судном. Исходной информацией для проведения вычислений может служить линейная скорость судна или его относительное ускорение. В обоих случаях для определения координат необходимо использование операций интегрирования, что приводит к появлению нестационарной ошибки. Наличие этой ошибки является существенным недостатком данного способа.

Параметры движения судна определяются как путем непосредственного их измерения, так и расчетным путем. Непосредственно можно измерить курс и углы качки судна, а также ускорение движения его центра масс и угловые скорости поворота судна*. А вот линейная скорость определяется косвенным методом:

· путем измерения напряжения, наводимого в морской воде специально созданным магнитным полем (индукционные лаги);

· измерением доплеровского сдвига частот отраженных от дна или слоев воды гидроакустических сигналов (доплеровские лаги);

· путем определения времени, затрачиваемого судном на прохождение определенного участка пути (корреляционные лаги).

Существуют и некоторые другие способы определения скорости, но они используются не так часто. В силу того, что для расчета скорости судна не требуется интегрирование измеренных значений, погрешности ее определения имеют стационарный характер.

В полном объеме навигационная информация может быть получена только от инерциальной навигационной системы (ИНС). Она представляет собой совокупность гироскопов и акселерометров, которые позволяют измерить текущую пространственную ориентацию судна и составляющие линейного ускорения его движения. Путем последующего интегрирования указанных ускорений определяется скорость судна и пройденный им путь.

ИНС автономны, т.е. могут решать задачи без привлечения для этого какой-либо внешней информации, однако, являясь системами счисления пути, в которых используются операции интегрирования, они имеют погрешности, нарастающие во времени. Это обстоятельство существенно ограничивает возможность автономного использования ИНС особенно на судах, где время движения достаточно велико.

Преодолеть указанную трудность можно или путем использования прецизионных (очень точных) гироскопов и акселерометров, или путем коррекции показаний системы по сигналам других навигационных приборов и систем. Реализация первого пути при создании морских навигационных систем в силу очень длительного времени плавания связана со значительными техническими и технологическими проблемами. К тому же такие системы становятся неприемлемо дорогими и практически бесперспективными для использования на транспортных судах.

Второй путь по оценкам специалистов [3,19,33] является наиболее перспективным для применения на морских судах в ХХI веке. Именно этот путь привел к разработке интегрированных систем ориентации и навигации (ИСОН).

Гироскопические системы могут использоваться для решения не всего комплекса навигационных задач, а лишь для получения информации об одном или нескольких параметрах движения судна. Так, гироскопические

компасы (ГК) определяют текущий курс судна, гирогоризонты (гировертикали) – положение плоскости горизонта, гиротахометры (ГТ) – угловую скорость поворота судна. Информация о текущем курсе судна и его угловой скорости используется для:

· удержания судна на заданном курсе;

· поворота судна на новый курс;

· обеспечения движения судна по заданной траектории.

Знание параметров пространственной ориентации судна позволяет:

· автоматически настроить авторулевой на оптимальный режим работы;

· построить на борту судна, стабилизированные в плоскости горизонта и по азимуту, платформы, на которых может размещаться оборудование, нуждающееся в указанной стабилизации;

· учитывать значения этих параметров при выполнении различных вычислений, связанных с решением навигационных задач.

Как видим, роль гироскопических систем в процессе управления движением судна и обеспечения безопасности мореплавания является ключевой. Поэтому в настоящее время во всех развитых странах уделяется серьезное внимание вопросам совершенствования этих систем.

Определение понятия “гироскоп”

Гироскопические явления были замечены человеком еще в древно-сти. Об этом свидетельствует, например, дошедшая до наших дней из глубины веков игрушка – волчок. С давних пор людей интересовало свойство волчка, вращающегося с угловой скоростью ω (рис. 2.1), оставаться устойчивым на своей острой точке опоры, сохраняя при этом направление оси неизменным даже в том случае, если поверхность, на которую он опирается, наклонить на некоторый угол β. Однако объяснение этих свойств стало возможным лишь значительно позже, ко-гда в ХVΙΙΙ веке Л. Эйлером были заложены основы механики движения твердого тела. Глубокое изучение закономерностей, которым подчиняется движение твердого тела, было обусловлено, прежде всего, задачами астрономии. Полученные Эйлером уравнения, описывающие вращение твердого тела вокруг центра масс, имели решающее значение для понимания гироскопических явлений и положили начало дальнейшим исследованиям в этой области.

В 1852 году известный физик Л. Фуко (1819 – 1868) осуществил подвес волчка с помощью двух кардановых колец, обеспечив, тем самым, неизменность положения точки опоры относительно его основания при любой пространственной ориентации этого основания. Использование карданового подвеса позволило придать волчку форму массивного ротора Р (рис. 2.2) [31] , свободно вращающегося вокруг так называемой главной оси подвеса ОА во внутреннем кардановом кольце ВК.

В свою очередь, кольцо ВК устанавливалось в наружном кольце НК подвеса с помощью двух опор, расположенных по оси ОВ. Благодаря такой схеме обеспечивалась свобода вращения ротора Р вместе с кольцом ВК в наружном кольце НК вокруг внутренней оси подвеса 0В. Наконец, наружное карданово кольцо НК, также с помощью двух опор, расположенных по оси ОС, устанавливалось на основании КП прибора, обеспечивая свободу вращения ротора Р вместе с обоими кардановыми кольцами ВК и НК вокруг наружной оси подвеса ОС.

Опыты, проведенные с новым прибором, показали, что он обладает теми же свойствами, которые присущи элементарному волчку. При со-общении ротору Р вращения с достаточно большой угловой скоростью вокруг оси ОА направление последней оставалось стабильным в пространстве. При установке же прибора на земной поверхности, на-пример на экваторе в некоторой точке L (рис. 2.3), его главная ось АА не сохраняет неизменным свое направление относительно земной поверхности. Вследствие суточного вращения Земли точка L будет непрерывно изменять свое положение в

пространстве, занимая последовательно положения L1, L2 и т. д. Вместе с Землей в ее суточном вращении будет участвовать и волчок, точка подвеса которого благодаря наличию карданового подвеса неподвижна относительно земной поверхности. Однако главная ось АА волчка, стремящаяся сохранить неизменным свое направление в мировом пространстве, будет в рассматриваемом случае непрерывно отклоняться от плоскости горизонта аа, составляя с последней угол, равный по величине углу поворота земного шара вокруг своей оси (рис. 2.3).

Прибор Фуко позволял по отклонению главной оси АА волчка от земных ориентиров, остающихся неизменными относительно плоскостей горизонта и меридиана, судить о вращении Земли. Он давал возможность «видеть» земное вращение, почему и был назван «гироскопом», т. е. прибором, позволяющим наблюдать вращение Земли.

Одновременно были выявлены и другие столь же замечательные свойства гироскопа. Так, затяжка винтов dв, расположенных на наружном кольце НК подвеса (рис. 2.2), лишала гироскоп свободы вращения вокруг оси 0В и создавала условия, при которых он стремился совместить свою главную ось ОА с плоскостью меридиана, что позволяло определить ее положение в данном пункте земной поверх-ности.

При затягивании стопорного винта dс на корпусе прибора гироскоп лишается свободы вращения вокруг оси ОС. В этом случае при определенных условиях его главная ось ОА стремится совместиться с направлением, параллельным земной оси, что позволяет использовать гироскоп для определения географической широты выбранной точки земной поверхности.

Общее представление об основных свойствах гироскопов можно получить, используя теорему о кинетическом моменте. Эта теорема фактически является формулировкой первого закона И. Ньютона для вращательного движения. Действительно, названный закон аналитически можно представить в следующем виде:

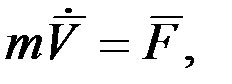(2.1)

где m – масса движущегося линейно тела, 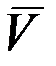– скорость его движения, 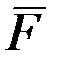– сила, приложенная к телу. Физический смысл этого закона заключается в том, что изменение вектора скорости движущегося тела происходит только в том случае, если на него действует какая-либо приложенная извне сила.

Используя выражение (2.1) и аналогии между параметрами, характеризующими поступательное и вращательное движение (см. приложение П1), запишем:

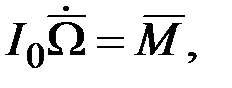(2.2)

где I₀ – момент инерции тела относительно оси вращения, – угловая скорость вращения тела, 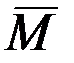- вектор момента внешней силы, приложенный к телу. Равенство (2.2) представляет собой математическую формулировку теоремы о кинетическом моменте вращающегося тела. Если учесть, что

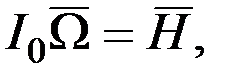(2.3)

где 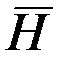– вектор кинетического момента этого тела, то выражение (2.2) можно переписать в виде:

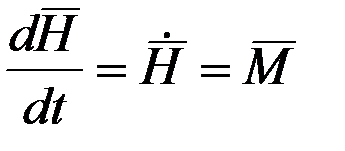. (2.4)

Принимая во внимание, что 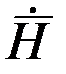определяет скорость конца вектора кинетического момента, т.е. изменение этого вектора по модулю и направлению, можно утверждать, что это изменение имеет место лишь в том случае, если на тело действует момент внешней силы. Действительно, если 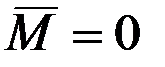, то вектор 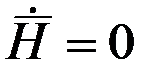и кинетический момент гироскопа остается неизменным как по величине, так и по направлению.

Важно!

Гироскоп, на ротор которого не действуют никакие моменты внешних сил, называют свободным. Учитывая это, можно сформулировать первое свойство гироскопов – свободный гироскоп сохраняет ось вращения своего ротора (главную ось) неизменно ориентированной в пространстве. Это свойство имеет большое практическое значение, так как из него вытекает возможность построения на борту подвижного объекта автономной ортогональной системы координат, не вращающейся в пространстве или изменяющей свою ориентацию заранее заданным образом. Указанное обстоятельство дало мощный толчок для развития инерциальных навигационных систем.

Второе свойство гироскопа определяет его поведение при воздействии постоянных моментов внешних сил. Рассмотрим случай, когда момент М, приложенный к ротору гироскопа, имеет относительно него произвольную ориентацию (рис. 2.10). Этот момент можно представить составляющими М_х, М_у и М_z, направленными вдоль осей ох, оу и oz, соответственно. Составляющая М_х будет вызывать изменение кинетического момента гироскопа, скорость которого 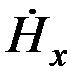направлена вдоль оси ох так же, как и вектор 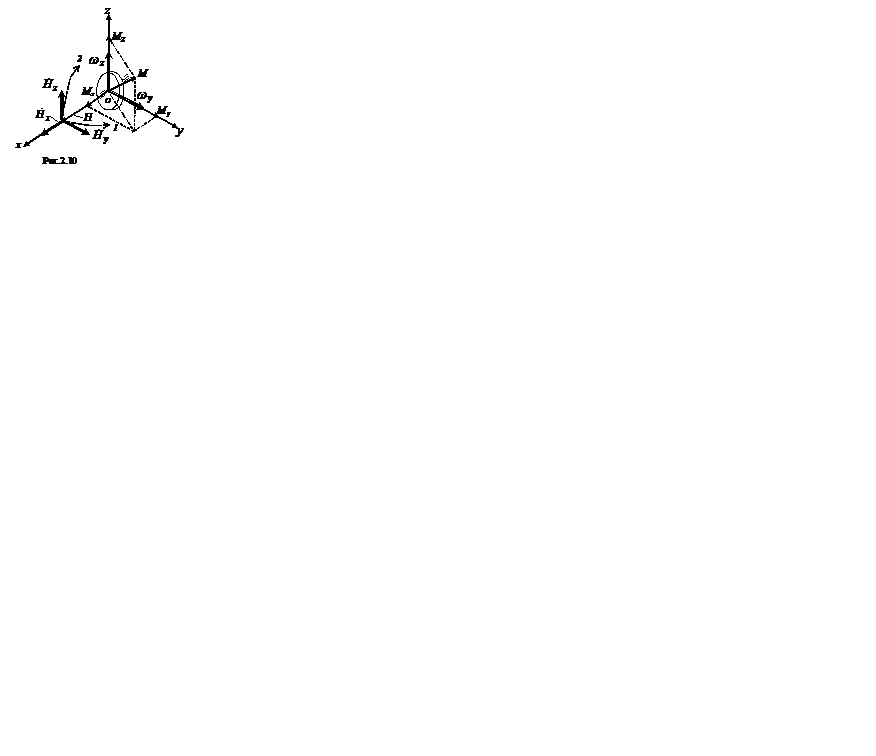Н. Данное обстоятельство свидетельствует о том, что указанная составляющая момента внешних сил не оказывает влияния на направление вектора Н, а изменяет только его модуль. Поскольку величина осевого момента инерции ротора гироскопа остается постоянной, то будет происходить изменение скорости вращения ротора. Таким образом, теорема о кинетическом моменте позволила выявить довольно очевидный факт – момент внешней силы, приложенный относительно главной оси гироскопа, изменяет скорость вращения его ротора.

Важно!

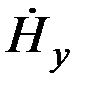Совсем иное воздействие на ротор оказывают составляющие момента, направленные по осям оу и oz. Момент М_у в соответствие с рассматриваемой теоремой вызывает изменение кинетического момента, вектор которого равен и параллелен М_у. В силу того, что вектор 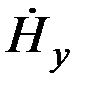перпендикулярен оси ох, изменение модуля кинетического момента гироскопа (числа оборотов ротора) происходить не будет, а будет иметь место изменение направления вектора Н с некоторой угловой скоростью ω. При этом 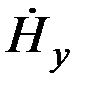будет определяться следующим равенством:

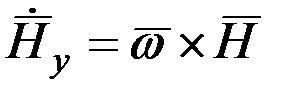. ( 2.5)

В соответствие с правилами умножения вектор 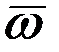должен быть перпендикулярен векторам 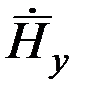и 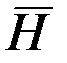и направлен в ту сторону откуда вращение вектора 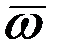к вектору 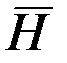по кратчайшему пути наблюдается происходящим против часовой стрелки. Таким образом, в рассматриваемом случае вектор 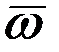будет направлен по оси oz вверх и, следовательно, гироскоп будет поворачиваться с угловой скоростью ω_z (рис. 2.10) в направлении, показанном штриховой стрелкой 1. Это движение гироскопа получило название прецессии. Как видим, под действием составляющей М_у момента внешних сил, стремящейся повернуть ротор гироскопа вокруг оси оу, гироскоп не будет поворачиваться вокруг этой оси, а начнет прецессировать (поворачиваться) вокруг оси oz, как бы пытаясь совместить вектор 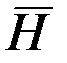с вектором рассматриваемой составляющей момента внешней силы.

Можно показать, что аналогичной будет реакция гироскопа и на составляющую М_z внешнего момента. Под ее действием гироскоп начнет прецессировать вокруг оси оу с угловой скоростью ω_у в направлении, показанном штриховой стрелкой 2, стремясь совместить 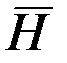с вектором М_z.

Важно!

Обобщая сказанное, можно сформулировать следующее правило прецессии гироскопа: “Если на ротор гироскопа действует момент внешней силы вокруг оси, не совпадающей с главной, то он начинает прецессировать таким образом, чтобы кратчайшим путем совместить вектор своего кинетического момента с вектором момента внешней силы.”

Используя указанное правило легко найти направление прецессии оси гироскопа. Пусть к гироскопу приложена некоторая сила F (рис. 2.11). Для решения поставленной задачи следует определить направление момента М_z этой силы (см. приложение П.1) и воспользоваться приведенным правилом. В

результате нетрудно установить, что прецессия гироскопа будет происходить вокруг оси оу с угловой скоростью ω_у.

Следующее свойство определяет поведение гироскопа при действии на него импульса момента внешней силы (удара). Если считать, что этот момент приложен к гироскопу в течение короткого промежутка времени 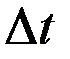, то, используя теорему о кинетическом моменте, можно записать:

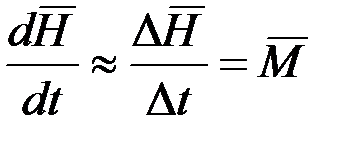или 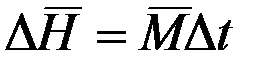, (2.6)

Важно!

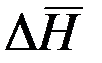где - изменение вектора кинетического момента гироскопа за время 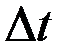действия момента 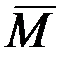. Учитывая, что это время мало, даже при относительно больших величинах внешних моментов изменение кинетического момента гироскопа будет оставаться незначительным. Отсюда можно сделать вывод, что действие на гироскоп импульса момента силы не приводит к существенному изменению вектора его кинетического момента.