Принцип действия доплеровского лага

Принцип действия доплеровских лагов основан на определении скорости судна по доплеровским сдвигам частот акустических сигналов, излучаемых с борта дви­жущегося судна и принятых антенной системой судна после отражения их от морского дна.

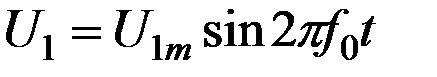Предположим, что акустическая волна, возбуждаемая антенной А (рис. 3.1) лага, установленного на судне, движущемся со скоростью v, распространяется в сторону морского дна под острым углом a по отноше­нию к вертикали АВ. Для формирования указанной волны на антенну подается напряжение с частотой f_o и амплитудой U_1m. Достигнув точки С, волна отразится от дна и часть звуковой энергии, вернувшейся на судно будет принята антенной лага. При этом на выходе приемной антенны появится напряжение:

(3.1)
где U_2m – амплитуда принятого сигнала, y - отставание по фазе принятого сигнала от излучаемого.

Будем считать, что амплитуда принятого сигнала достаточна для того, чтобы выделить сигнал из помех и проводить дальнейшую его обработку. Фаза сигнала определяется временем Dt движения луча до дна и обратно:

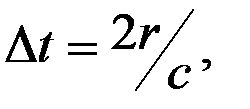(3.2)
где r – расстояние от антенны до точки С, а с – скорость звука.

За счет движения судна на интервале времени Dt происходит непрерывное изменение расстояния АС. Закон изменения этого расстояния можно записать в виде:

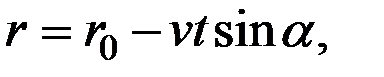(3.3)
где r₀ – начальное значение расстояния АС. Учитывая, что фазовый сдвиг

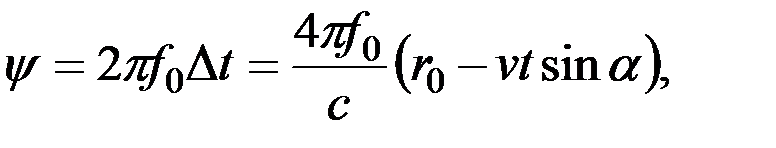(3.4)
выражение (3.1) перепишем в виде:

(3.5)
где 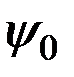- фазовый сдвиг, равный:

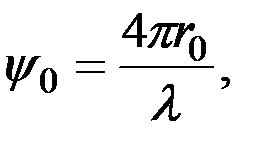(3.6)
а l - длина волны излучаемого сигнала. Как известно

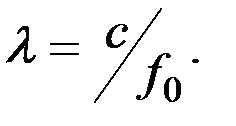(3.7)

Из равенства (3.5) видно, что частота принятого антенной сигнала возросла на величину доплеровского сдвига

(3.8)
которая пропорциональна скорости движения судна. Поэтому, измеряя значение f_д можно найти интересующую нас скорость:

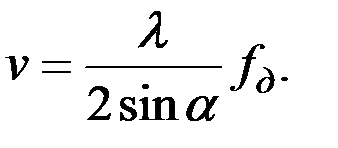(3.9)

Формула (3.9) указывает на линейную зависимость скорости судна от доплеровского сдвига частоты. Как и в большинстве реальных физических процессов, в дейст­вительности между скоростью судна и доплеровским сдвигом существует нелинейная зависимость.

Прием акустических колебаний производится после отражения их от морского дна, которое представляет собой источник большого числа элементарных отража­телей. Поэтому при отражении происходит изменение расстояния между приемопередающей антенной лага и отдельными элементарными отражателями. Элемен­тарные сигналы, принятые от множества отражателей морского дна, имеют случайные начальные фазы.

Углы a, под которыми с борта судна визируются эле­ментарные отражатели морского дна, отличаются друг от друга в пределах лепестка диаграммы направленно­сти, что также приводит к различию доплеровских сдвигов отдельных элементарных сигналов. Поэтому принятый антенной лага сигнал представляет собой сумму элементарных отраженных сигналов и определяется не одной частотой, а спектром частот (доплеровским спектром). Положение этого спектра на оси частот относительно частоты излучения характеризуется средней доплеровской частотой f_{д ср.}, определяемой как разность средней частоты спектра f_cp и частоты излучения f_o.

Более точной формулой для определения частоты f принятого отраженного элементарного сигнала является выражение [17]:

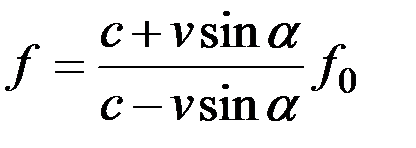, (3.10)

которое можно разложить в ряд:

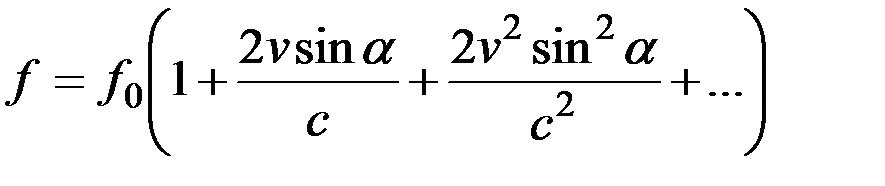. (3.11) При этом, если ограничиться тремя членами ряда, доплеровский сдвиг частоты будет иметь вид:

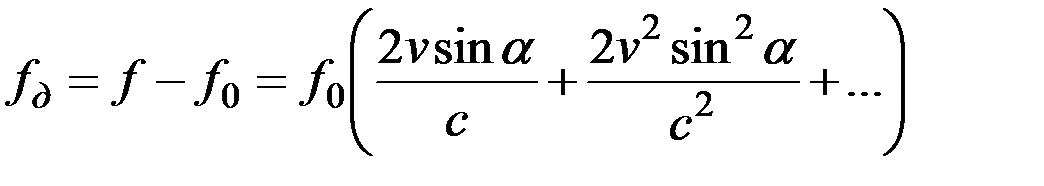(3.12)

Формула (3.12) выражает нелинейную зависимость между доплеровским сдвигом частоты и скоростью судна. Однако величина этой нелинейности не велика, так как скорость звука значительно превышает скорость судна.

Для устранения указанной нелинейности и исключения влияния изменений углов a, возникающих в результате качки судна и ряда других причин, используется двухлучевая антенная систе­ма (рис. 3.2). Частоты принятых сигналов по носовому 1 и кормовому 2 лучам определяются следующими выражениями:

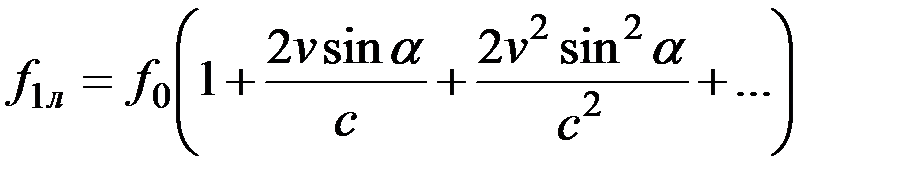(3.13)

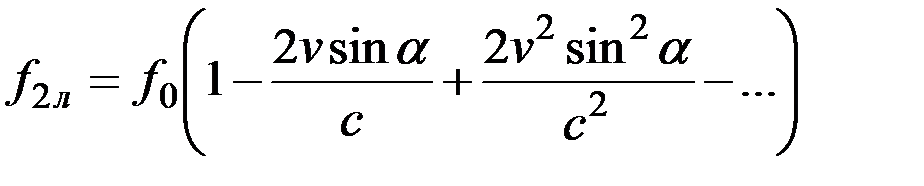(3.14)

Их разностная частота будет равна:

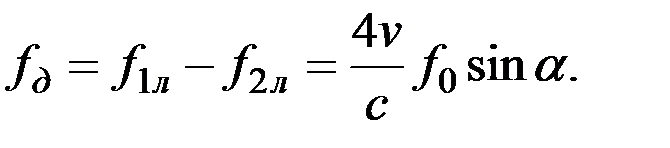(3.15)

В рассматриваемом случае выражение для определения скорости приобретает вид:

(3.16)

Для двухлучевой антенной системы доплеровский сдвиг частоты практически линейно зависит от скоро­сти, что уменьшает погрешности измерений.

В том случае, если судно идет с некоторым углом дифферента q (рис. 3.3), доплеровские сдвиги частот по лучам будут определяться следующими равенствами:

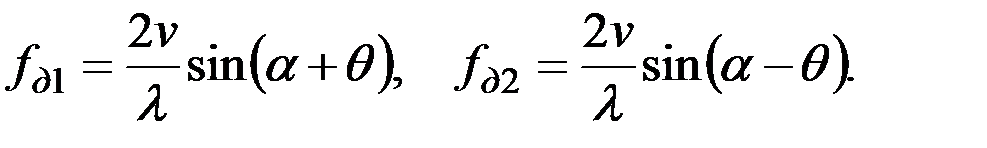(3.17)

В этих условиях выражение для разности доплеровских сдвигов частот может быть записано в виде:

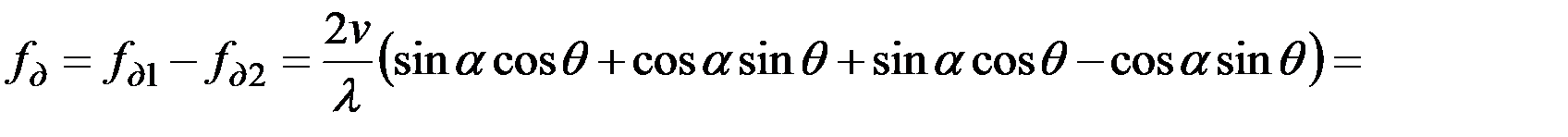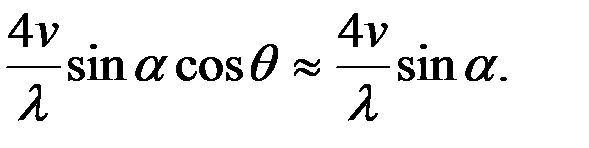= (3.18)

Приближение, принятое здесь, допустимо ввиду малости отличия значения cosq от единицы при имеющих место на практике углах дифферента. Как следует из выражения (3.18) разность доплеровских сдвигов частот, которая используется для вычисления скорости судна, практически не зависит от угла θ. На рис. 3.4 приведены значения относительной погрешности измерения скорости судна при использовании однолучевой (кривая 1) и двухлучевой (кривая 2) систем. Из графика видно, что использование двухлучевой системы практически полностью устраняет погрешность, обусловленную углами дифферента судна.

В связи с необходимостью измерения не только продольной скорости судна, но и поперечной довольно широко стали применяться многолучевые антенные системы. Наибольшее распространение среди них получили четырехлучевые системы с диаметрально–траверсной (рис. 3.5, а) и “X” – образной (рис. 3.5, б) схемами расположения лучей. В первом случае скорость судна вычисляется аналогично тому, как это делается в двухлучевой системе. Для каждой составляющей скорости используется своя пара лучей:

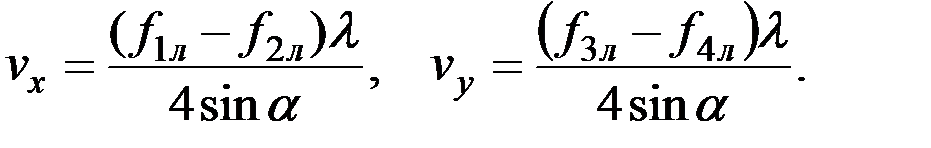(3.19)

При использовании более информативной “X” – образной схемы расположения лучей каждая составляющая скорости определяется по сигналам всех четырех лучей:

(3.20)

В случае отсутствия сигнала по одному из лучей имеется возможность изменить алгоритм вычисления составляющих скорости судна при сохранении практически той же погрешности получаемого результата. Так, при отсутствии отраженного сигнала второго луча вычисление составляющих скорости может производиться, используя следующие равенства:

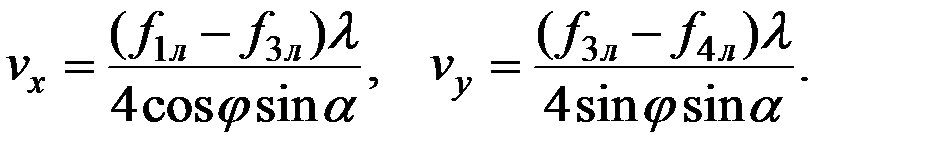(3.21)

Аналогично могут быть изменены алгоритмы вычисления составляющих скорости судна при отсутствии сигнала по другим лучам. При указанных изменениях сохраняется методика определения, присущая двухлучевой системе.

Наряду с четырех лучевой используются и трех лучевые системы, сохраняющие в основном достоинства схемы Януса, но позволяющие упростить аппаратную часть лага за счет снижения количества каналов, необходимых для обработки принятого сигнала (рис. 3.6). Составляющие скорости судна в рассматриваемом случае определяются по следующим зависимостям [17]:

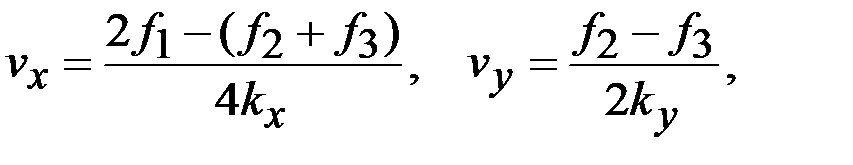(3.22)
где f₁, f₂ и f₃ – частоты принятых сигналов по соответствующим лучам, k_x и k_y – коэффициенты передачи соответствующих каналов.

Принцип действия корреляционного лага

Принцип действия корреляционного лага основан на измерении времени, затрачиваемого судном на прохождение определенного участка пути, длина которого определяется расстоянием между вибраторами гидроакустической антенны лага и принятым алгоритмом обработки информации.

t

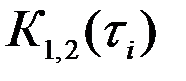
УС

И

МУ

БЗ

В

УИ

УП1

УП2

ПУ

А2

А1

h

l

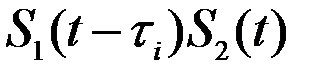
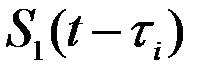
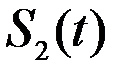
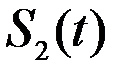
S1(t)

U

τm

U1(t)

U2(t)

Рис.1.71

Рис.1.70

Предположим, что на судне вдоль диаметральной плоскости (ДП) размещены две гидроакустические приёмно – передающие антенны А1 и А2 (рис. 1.70) на расстоянии l друг от друга. В режиме излучения эти антенны совместно с передающим устройством (ПУ) формируют импульсы, которые распространяются в сторону дна, отражаются от него и возвращаются обратно. Принимаемые антеннами сигналы будут зависеть от отражающей способности грунта, рельефа дна, от параметров среды их распространения и представлять собой некоторые случайные процессы U₁(t) и U₂(t), изменяющиеся во времени (рис.1.71). В связи с тем, что при отсутствии дрейфа судна антенна А2 проходит над теми же участками дна, что и антенна А1, процессы U₁(t) и U₂(t) будут аналогичны друг другу, но сдвинуты по времени на величину 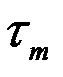, которая получила название транспортного запаздывания. Очевидно, величина транспортного запаздывания зависит от расстояния l между антеннами и скорости V движения судна. В рассматриваемом случае будет иметь место следующее равенство:

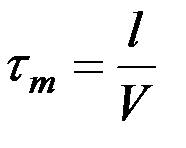. (4.1)

Отсюда может быть найдена скорость судна:

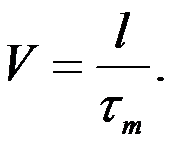(4.2)

Учитывая, что база l известна, задача определения скорости сводится к оценке значения транспортного запаздывания .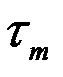

Транспортное запаздывание 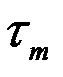определяется путём искусственной задержки сигнала первой антенны с помощью регулируемого блока задержки БЗ (рис. 1.70), который осуществляет смещение процесса U₁(t) (рис.1.71) вдоль оси времени. Для каждой задержки 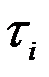рассчитывается значение ВКФ и эти значения сравниваются между собой. Очевидно, что при 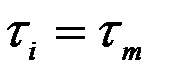, сдвиг сигнала первой антенны вдоль оси времени будет таким, что процессы практически совпадут и величина ВКФ будет максимальной.

Учитывая сказанное, каждый корреляционный лаг должен включать в себя (рис. 1.70):

· антенную систему А;

· передающее устройство ПУ;

· усилители – преобразователи УП для придания принятому сигналу вида, удобного для дальнейшей обработки;

· регулируемый блок задержки БЗ;

· коррелятор, состоящий из множительного устройства МУ и интегратора И;

· устройства сравнения УС значений корреляционных функций;

· вычислитель В скорости, пути, пройденного судном и других величин;

· устройства индикации УИ.

Рассмотрим особенности устройства отдельных систем лага.