Установка заготовки в центрах
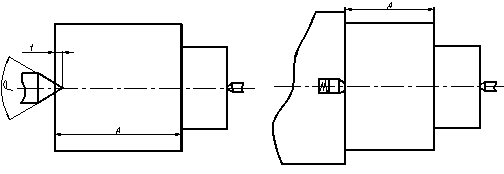 Установку заготовки в центрах производят либо тогда, когда передний центр жёсткий (рисунок 4,а), либо тогда, когда передний центр – плавающий, а задний – жёсткий (рисунок 4,б).
Установку заготовки в центрах производят либо тогда, когда передний центр жёсткий (рисунок 4,а), либо тогда, когда передний центр – плавающий, а задний – жёсткий (рисунок 4,б).
Рисунок 4 - Схема установки заготовок в центрах
При использовании жёсткого переднего центра наблюдается погрешность базирования в своём направлении, которая является следствием неточного изготовления центровых отверстий в этом направлении: Еб = Езац, где Езац – погрешность зацентровки центровых отверстий, мм (таблица 2).
Таблица 2
| Наибольший диаметр центрового гнезда, мм, с углом α = 60° | Значения погрешности Езац |
| 12 – 2,5 14 – 6 17,5 – 10 12,5 – 15 | 0,11 0,14 0,18 0,21 |
При применении плавающего центра Еб = 0. Погрешность базирования для диаметральных размеров в обеих случаях равна нулю. Погрешность закрепления Ез для диаметральных размеров равна нулю, а для осевых размеров при использовании жёсткого переднего центра определяется по формуле
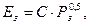 (5)
(5)
где С - коэффициент, учитывающий диаметр центрового гнезда и выбираемый по таблице 3.
Таблица 3
| Диаметр центрового гнезда, мм | Значение коэф. С |
| 7,5 12,5 | 8,6 4,1 2,9 2,5 2,2 1,6 1,3 1,1 |
При выполнении данной работы необходимо произвести обработку наружной поверхности в размер А до упора. Предварительно нужно провести измерение глубины зацентровочных отверстий с той стороны, где будет входить передний центр. Разность показаний глубины отверстий сравнить с табличными данными. Провести измерение полученных размеров А. Разность их представляет фактическую погрешность установки, которую необходимо сравнить с расчётной , определяемой по формуле (1); (5) и таблицам 2 и 3.
ИССЛЕДОВАНИЕ ТОЧНОСТИ МЕХАНИЧЕСКОЙ ОБРАБОТКИ МЕТОДАМИ ПОСТРОЕНИЯ ТОЧЕЧНЫХ ДИОГРАММ И ПО НАРАСТАЮЩИМ ОТКЛОНЕНИЯМ РАЗМЕРОВ.
Одним из методов исследования точности механической обработки является метод построения точечных диаграмм. При этом по оси абсцисс отмечают номера обрабатываемых деталей в той последовательности, в какой они обрабатывались, а по оси ординат откладывают в виде точек в определённом масштабе результаты измерений: диаметр, длина, угол и т.д. (рисунок 1). Для сокращения длинны точечных диаграмм, особенно для большой партии деталей, отмечают не номера деталей, а номера групп деталей (см. рисунок 1,б). В этом случае группы деталей должны быть одинаковыми по количеству деталей. Если учёт строгой последовательности обработки деталей в пределах каждой группы не имеет значения, то по оси ординат откладывается групповое среднее значение Хср. (рисунок 1,в). Учёт же последовательности групп деталей обязателен.
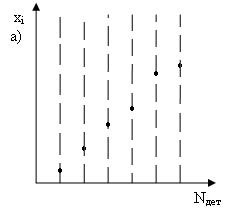
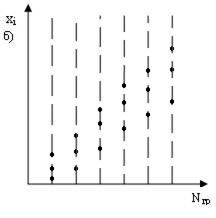
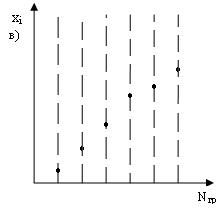
Рисунок 1 - Точечные диаграммы
Точечные диаграммы с учётом групповых результатов обработки деталей позволяют наиболее наглядно показать влияние на точность закономерно действующего фактора. Так, например, на подобных диаграммах отчётливо видна погрешность размеров в результате непрерывного протекающего износа режущей кромки инструмента. Выход точки за пределы поля допуска или её приближение к пределам служат сигналом о появлении брака детали и указывают на необходимость подналадки оборудования.
 Свойства точечных диаграмм изучаются подробно в связи с широким применением в промышленности статического метода контроля продукции. Сущность его заключается в том, что в процессе изготовления продукции периодически, то есть через определённые промежутки времени, берутся пробы для измерений в количестве от 2 до 10 деталей.
Свойства точечных диаграмм изучаются подробно в связи с широким применением в промышленности статического метода контроля продукции. Сущность его заключается в том, что в процессе изготовления продукции периодически, то есть через определённые промежутки времени, берутся пробы для измерений в количестве от 2 до 10 деталей.
Ъ
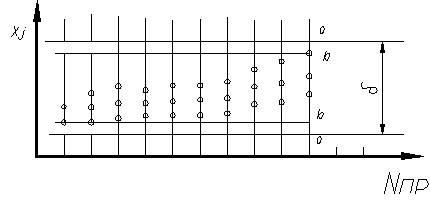
Рисунок 2 - Точечная диаграмма статического метода контроля
Результаты измерений наносятся на специальную контрольную диаграмму (рисунок 2), на которой сплошными параллельными линиями (а-а) отпечатано поле допуска, а штрихами (б-б)- контрольное поле допуска. При приближении измеренных точек к контрольному полю допуска необходимо производить подналадку инструмента относительно обрабатываемой детали. Расположение штрихов на диаграмме определяется на основе теоретических положений статического контроля.
Дальнейшим развитием точечных диаграмм является построение и анализ точечных диаграмм (рисунок 3).
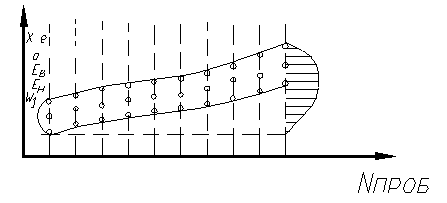 |
Рисунок 3 - Точечная диаграмма
В этом случае для каждой группы проб последовательно обработанных деталей находят:
Хср.- среднее арифметическое отклонение:
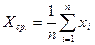 , (1)
, (1)
где n - количество деталей в группе; xi – текущий размер детали в группе; σ - среднее квадратическое отклонение; Ев, Ен- верхнее и нижнее отклонения от среднего арифметического (разность этих отклонений есть поле рассеивания для каждой группы).
По оси абсцисс откладывают номер последовательно взятой группы проб, а по оси ординат- вычисленные значения Хср., σ, Ев, Ен. Соединяя соответствующие точки , получают ломанные линии, характеризующие измерения указанных выше величин при протекании исследуемого процесса обработки. Проведя такие наблюдения для нескольких партий, можно получить надёжную точностную диаграмму.
Обычно распределение размеров в пределах одной группы отвечает нормальному закону, для всей же совокупности деталей может от него отличатся в силу большого или меньшего влияния систематической закономерно изменяющейся погрешности. Так, например, при изменении Хср. по закону прямой линии, наклонной под углом к оси абсцисс (размерный износ инструмента), распределение по всей совокупности будет характеризоваться плосковершинной кривой. При рассмотрении значений Хср. По закону параболы величина систематической погрешности может быть выражена уравнением кривой второго прядка. Постоянное и периодическое действие во времени сразу нескольких систематических факторов приводит к целому семейству теоретических кривых распределения, подробно рассмотренных профессором Н.А. Бородачёвым.
К недостатку метода по нарастающим отклонениям размеров следует отнести то, что при наличии нескольких закономерно изменяющихся систематических погрешностей последние трудно разделимы, а поэтому их влияние на суммарную погрешность оценивается комплексно. Кроме того, для исследования точностными диаграммами требуется сравнительно большее количество наблюдений.
Для анализа точности обработки по нарастающим отклонениям размеров используются те же результаты обработки деталей, которые были получены при использовании точечных диаграмм. Вначале по формуле (1) определяют среднее арифметическое значение размеров деталей и округляют его до знака, на который оканчиваются фактические размеры заготовок. Для чистовой обработки значения округляют обычно до 0,01 мм. Далее для каждого значения n =1…50 находят накапливающую арифметическую среднюю Хн по формуле
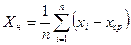 , (2)
, (2)
Строится график зависимости, например Хн = f(n) (рисунок 4), и проводится его анализ.
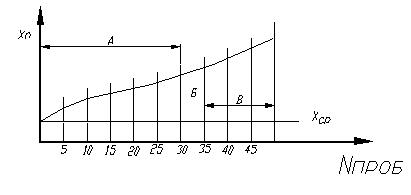
Рисунок 4 - График зависимости Хн = f(n)
Из анализа данного графика можно сделать следующие выводы:
1. Наличие постепенного подъёма кривой указывает на действие определенной систематически действующей погрешности, вызванной размерным износом инструмента.
2. Затухающая форма участка А кривой говорит о влиянии причины периодического характера в зависимости от времени. На рисунке 5 показано влияние этой причины на Хн. По оси абсцисс отложено время работы станка, по оси ординат – размеры деталей (кривая 1) и средняя арифметическая Хн (кривая 2).
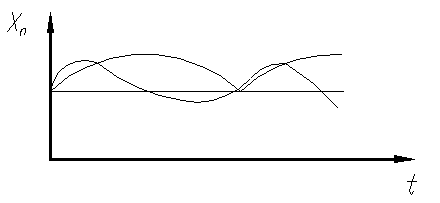
Рисунок 5 - Влияние причины периодического характера на Хн
Причина данного характера имеет место при эксцентрическом вращении частей станка, влияющих на размер детали. В частности, подобное явление имеет место при эксцентрическом вращении ведущего круга бесцентрово-шлифовального станка.
3. Заметный подъём в т. Б свидетельствует о появлении длительно действующей постоянной погрешности, которой может быть например, частичное регулирование станка.
Достоинства данного метода оценки точности обработки детали следующие:
Метод позволяет обнаружить систематические погрешности, дать им количественную оценку и наметить меры по их устранению;
Позволяет выявить периодические колебания.
К недостаткам метода следует отнести затухающий характер кривой, который не позволяет выявить влияние отдельных факторов на точность обработки.
Дата добавления: 2017-02-13; просмотров: 2885;











