Понятие соответствия. Способы задания соответствий

Первоначально алгеброй называли учение о решении уравнений. За много столетий своего развития алгебра превратилась в науку, которая изучает операции и отношения на различных множествах. Поэтому не случайно уже в начальной школе дети знакомятся с такими алгебраическими понятиями, как выражение (числовое и с переменными), числовое равенство, числовое неравенство, уравнение. Они изучают различные свойства арифметических действий над числами, которые позволяют рационально выполнять вычисления. И, конечно, в начальном курсе математики происходит их знакомство с различными зависимостями, отношениями, но чтобы использовать их в целях развития мыслительной деятельности детей, учитель должен овладеть некоторыми общими понятиями современной алгебры - понятием соответствия, отношения, алгебраической операции и др. Кроме того, усваивая математический язык, используемый в алгебре, учитель сможет глубже понять сущность математического моделирования реальных явлений и процессов.

Изучая окружающий нас мир, математика рассматривает не только его объекты, но и главным образом связи между ними. Эти связи называют зависимостями, соответствиями, отношениями, функциями. Например, при вычислении длин предметов устанавливаются соответствия между предметами и числами, которые являются значениями их длин; при решении задач на движение устанавливается зависимость между пройденным расстоянием и временем, если скорость движения постоянна.

Конкретные зависимости, соответствия, отношения между объектами в математике изучались с момента ее возникновения. Но вопрос о том, что общее имеют самые разные соответствия, какова сущность любого соответствия, был поставлен в конце XIX - начале XX века, и ответ на него был найден в рамках теории множеств.

В начальном курсе математики изучаются различные взаимосвязи между элементами одного, двух и более множеств. Поэтому учителю надо понимать их суть, что поможет ему обеспечить единство в методике изучения этих взаимосвязей.

Рассмотрим три примера соответствий, изучаемых в начальном курсе математики.

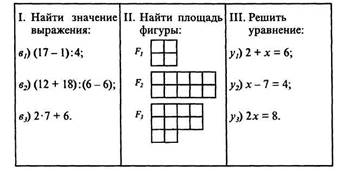
В первом случае мы устанавливаем соответствие между заданными выражениями и их числовыми значениями. Во втором выясняем, какое число соответствует каждой из данных фигур, характеризуя ее площадь. В третьем ищем число, которое является решением уравнения.

Что общее имеют эти соответствия?

Видим, что во всех случаях мы имеем два множества: в первом - это множество из трех числовых выражений и множество N натуральных чисел (ему принадлежат значения данных выражений), во втором - это множество из трех геометрических фигур и множество N натуральных чисел; в третьем - это множество из трех уравнений и множество N натуральных чисел.

Выполняя предложенные задания, мы устанавливаем связь (соответствие) между элементами этих множеств. Ее можно представить наглядно, при помощи графов (рис. 1).

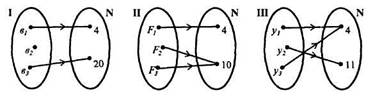
Можно задать эти соответствия, перечислив все пары элементов, находящихся в заданном соответствии:

I. {(в₁, 4), (в₃, 20)};

II. {( F₁, 4), (F₂, 10), (F₃, 10)};

III. {(у₁, 4), (у₂, 11), (у₃, 4)}.

Полученные множества показывают, что любое соответствие между двумя множествами X и Y можно рассматривать как множество упорядоченных пар, образованных из их элементов. А так как упорядоченные пары - это элементы декартова произведения, то приходим к следующему определению общего понятия соответствия.

Определение. Соответствием между элементами множество X и Y называется всякое подмножество декартова произведения этих множеств.

Соответствия принято обозначать буквами Р, S, T, R и др. Если S - соответствие между элементами множеств X и Y, то, согласно определению, S Х х Y.

Выясним теперь, как задают соответствия между двумя множествами. Поскольку соответствие - это подмножество, то его можно задавать как любое множество, т.е. либо перечислив все пары элементов, находящихся в заданном соответствии, либо указав характеристическое свойство элементов этого подмножества. Так, соответствие между множествами X = {1, 2, 4, 6} и Y = {3, 5} можно задать:

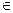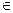1) при помощи предложения с двумя переменными: а < b при условии, что а X, b Y;

2) перечислив пары чисел, принадлежащих подмножеству декартова произведения XxY: {(1, 3), (1, 5), (2, 3), (2, 5), (4, 5)}. К этому способу задания относят также задание соответствия при помощи графа (рис. 2) и графика (рис. 3)

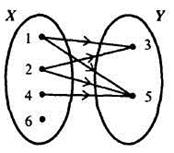
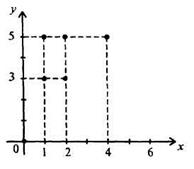
Рис. 2 Рис. 3

Нередко, изучая соответствия между элементами множеств X и Y, приходится рассматривать и соответствие, ему обратное. Пусть, например,

S - соответствие «больше на 2» между элементами множеств

Х = {4,5,8, 10} и Y= {2,3,6}. Тогда S={(4, 2), (5,3), (8, 6)} и его граф будет таким, как на рисунке 4а.

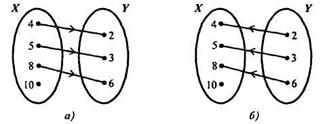
Рис.4

Соответствие, обратное данному, - это соответствие «меньше на 2». Оно рассматривается между элементами множеств Y и X, и чтобы его представить наглядно, достаточно на графе отношения S направление стрелок поменять на противоположное (рис. 4б). Если соответствие «меньше на 2» обозначить S^-1, то S^-1 = {(2,4), (3,5), (6,8)}.

Условимся предложение «элемент х находится в соответствии S с элементом у» записывать кратко так: xSy. Запись xSy можно рассматривать как обобщение записей конкретных соответствий: х = 2у; х > 3у+1 и др.

Воспользуемся введенной записью для определения понятия соответствия, обратного данному.

Определение. Пусть S - соответствие между элементами множеств X и Y. Соответствие S^-1 между элементами множеств Y и X называется обратным данному, если yS^-x тогда и только тогда, когда xSy.

Соответствия S и S^-1 называют взаимно обратными. Выясним особенности их графиков.

Построим график соответствия S = {(4, 2), (5, 3), (8, 6)} (рис. 5а). При построении графика соответствия S^-1 = {(2, 4), (3, 5), (6, 8)} мы должны первую компоненту выбирать из множества Y = {2, 3, 6}, а вторую - из множества X = {4, 5, 8, 10}. В результате график соответствия S^-1 совпадет с графиком соответствия S. Чтобы различать графики соответствий S и S^-1,

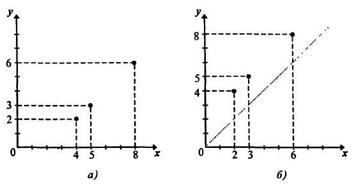
Рис.5

условились первую компоненту пары соответствия S^-1 считать абсциссой, а вторую - ординатой. Например, если (5, 3) 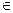S, то (3, 5) 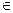S^-1. Точки с координатами (5, 3) и (3, 5), а в общем случае (х, у) и (у, х) симметричны относительно биссектрисы 1-го и 3-го координатных углов. Следовательно, графики взаимно обратных соответствий S и S^-1 симметричны относительно биссектрисы 1-го и 3-го координатных углов.

Чтобы построить график соответствия S^-1, достаточно изобразить на координатной плоскости точки, симметричные точкам графика S относительно биссектрисы 1-го и 3-го координатных углов.