Теоретические основы расчета вантовых мостов
Особенности статического расчета вантовых мостов
Главная особенность статического расчета вантовых мостовзаключается в возможности выключения гибких вант из работы при возникновении в них сжимающих усилий (рис. 13.1, а). В этом случае необходимо повторить расчет, рассмотрев новую конструкцию без выключенной ванты (рис. 13.1, б). При проектировании реального моста, безусловно, необходимо избегать подобной ситуации.
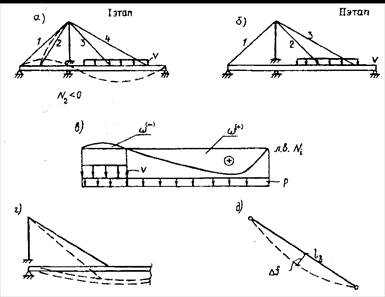
Рис. 13.1. Особенности расчета вантовых мостов
Рассмотрим линию влияния усилия в произвольной ванте Ni (рис. 13.1, в). В худшем случае загружения отрицательного участка временной нагрузкой получим величину
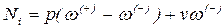 . (13.1)
. (13.1)
Первое слагаемое дает растяжение в ванте, а второе - сжатие. Поэтому для обеспечения стабильной работы ванты необходимо выполнить условие:
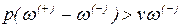 или
или 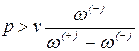 . (13.2)
. (13.2)
На практике это выглядит следующим образом: допустим, w(+) = 1 м, w(-) = 0,1 м, тогда при р > 0,1v/(1-0,1) = v/9 ванта будет работать только на растяжение.
Второе отличие расчета вантовых мостов от висячих состоит в том, что в связи с большей жесткостью их допускается рассчитывать без учета геометрической нелинейности. Это обусловлено еще двумя причинами:
- отсутствием S-образного изгиба при загружении части пролета;
- прямолинейностью вант (рис. 13.1, г).
Теоретически возможен учет геометрической нелинейности для вантовых мостов, которая в них имеет место хотя бы за счет провисания вант (рис. 13.1, д) под действием собственного веса. Но на практике эта величина невелика, так как в вантах провисание «выбирается» при регулировании усилия в них (см. далее).
Статический расчет вантовых мостов методами строительной механики
Вантовые конструкции представляют собой многократно статически неопределимые системы, если ванты рассматривать как стержни с осевой жесткостью ЕкАв и с изгибной жесткостью ЕкIв = 0.
Известно, что для расчета стержневых статически неопределимых систем в строительной механике существует три метода:
1) метод сил (основная система получается путем введения лишних неизвестных Xi: усилий в вантах, изгибающих моментов в балке, рис. 13.2, б),
2) метод перемещений (основная система получается путем введения жестких заделок в узлы конструкций, в качестве искомых неизвестных используются углы поворота и перемещения этих заделок Zi, рис. 13.2, в),
3) смешанный метод, который представляет собой комбинацию двух предыдущих методов и использует частично Xi , частично Zi.
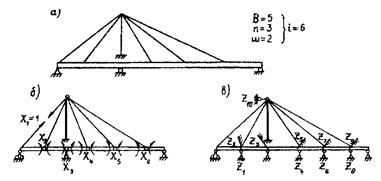
Рис. 13.2. Общая схема расчета вантовых мостов
Степень статической неопределимости вантовой системы при расчете методом сил можно определить по формуле (см. рис. 13.2, а):
i = B +2n - ш - 3, (13.3)
где В - число вант (В = 5 на рис. 3.13, а); n - число опор балки жесткости (n = 3); ш - количество подвижных опираний, включая подвижные опирания вант на пилонах (ш = 2). Конструкция, изображенная на рис. 13.2, a (i =5+2·3-2-3), шесть раз статически неопределима. Кстати, та же система, рассчитываемая методом перемещений, имеет 10 неизвестных Zi (рис. 13.2, в).
Рассмотренные расчетные схемы предполагают решение задачи в плоской постановке. Реальная задача расчета современных вантовых мостов гораздо сложнее, так как в них широко используются пространственные системы и балки жесткости, представляющие собой тонкостенные конструкции.
Расчет вантового моста требует последовательного использования расчетных схем, различных по уровню детализации проектируемой системы: плоская постановка задачи - пространственная расчетная схема - пластинчато-стержневая модель балки (решаемая численными методами прикладной теории упругости) - деформационный расчет пилона на устойчивость с учетом его неоднородности и начальных искривлений и т.д.
Подробнее с современной постановкой расчета вантовых мостов можно ознакомиться в книге [Вантовые мосты / А.А. Петропавловский, Е.И. Крыльцов, Н.Н. Богданов и др.; Под ред. А.А. Петропавловского. М.: Транспорт, 1985. 224 с., гл. 5-8]. Там отмечается, что наиболее широко применяют те или иные модификации основных методов строительной механики. Все большее применение получает метод конечных элементов, обладающий большой гибкостью и позволяющий получать решения практически для любых конструкций. Данный метод решает и специальные вопросы: распределение напряжений в местах анкеровки вант; развитие трещин в железобетонных балках и т. д.
Недостатки метода конечных элементов вытекают из его достоинств: увеличение числа неизвестных, приближение расчетных схем к реальным сооружениям приводят к большим затратам машинного времени мощных ЭВМ, сильно затрудняют обозримость результатов.
Анализ линий влияния внутренних усилий и прогибов в вантовых системах
В связи с тем, что обычно вантовые мосты рассчитывают без учета геометрической нелинейности, основной метод расчета заключается в построении линий влияния.
На рис. 13.3 приведены линии влияния прогибов и внутренних усилий для двухпролетной вантовой системы [Качурин В. К., Брагин А.В., Ерунов Б. Г. Проектирование висячих и вантовых мостов. М.: Транспорт, 1971. 280 с.]. Отметим некоторые особенности:
- площадь положительных участков на порядок больше отрицательных;
- очертания л. в. Ni и hi - гладкие, а л. в. Мi имеет пик в точке построения;
- загружение главного пролета временной нагрузкой является самым опасным;
- большое значение имеет установка опорной ванты, что снижает величины Мi, hi в 1,5...2 раза за счет уменьшения отклонения вершины пилона (рис. 13.3, б).
Площадь сечения опорной ванты назначают в 2...4 раза больше остальных.
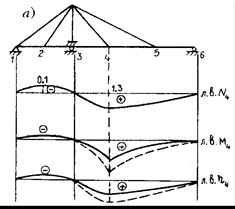
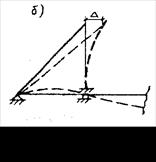
Рис. 13.3. Линии влияния двухпролетного вантового моста:
- - с опорной вантой; - - - - без нее
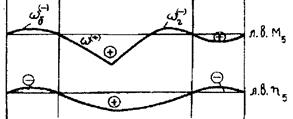
На рис. 13.4 показаны очертания линий влияния аналогичных величин для трехпролетного вантового моста. Как видно, они принципиально не отличаются от рассмотренных выше линий влияния, но число участков у них больше.
На рис. 13.4 приведены также приближенные значения площадей основных участков по данным [Качурин В. К., Брагин А.В., Ерунов Б. Г. Проектирование висячих и вантовых мостов. М.: Транспорт, 1971. 280 с.], которые можно использовать при эскизном проектировании.
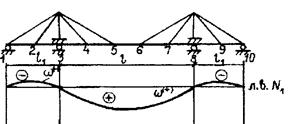
| w(+)» (0,60...0,65)l w(-)» (0,10...0,20)l |

| wг(+)» (0,30...0,35)l wб(+)» (0,002...0,05)l |
| w(+)» (0,0075...0,008)l2 wг(-)» (0,0030...0,0035)l2 wб(-)» (0,0010...0,0012)l2 |
Рис. 13.4. Линии влияния трехпролетного вантового моста
Регулирование внутренних усилий в балке жесткости вантовых мостов
Под термином «регулирование усилий» понимается совокупность мероприятий, обеспечивающих оптимальное распределение усилий в элементах вантово-балочных мостов и проектное положение оси балки.
Регулирование усилий производится, как правило, во время монтажа или перед началом эксплуатации моста. Для этого может использоваться один из способов:
1) предварительное натяжение вант;
2) поддомкрачивание балки при помощи временных промежуточных опор;
3) установка временных шарниров на время монтажа аналогично висячим мостам, но следует иметь в виду, что наклонное расположение вант может привести к потере устойчивости балки с шарнирами.
Главной целью регулирования усилий является уменьшение изгибающих моментов в балке жесткости до 1,5...2 раз. На рис. 13.5 показаны очертания эпюр изгибающих моментов в балке жесткости до регулирования усилий и после.
Учитывая, что в главном пролете преобладают положительные изгибающие моменты, балку необходимо предварительно выгнуть вверх, т.е. придать ей дополнительные отрицательные изгибающие моменты [Вантовые мосты / А.А. Петропавловский, Е.И. Крыльцов, Н.Н. Богданов и др.; Под ред. А.А. Петропавловского. М.: Транспорт, 1985. 224 с.].
Полученное очертание огибающей эпюры М позволяет существенно уменьшить расход материалов на балку жесткости (см. рис. 13.5 - новая эпюра М пунктиром), увеличив несколько усилия в вантах и пилоне.
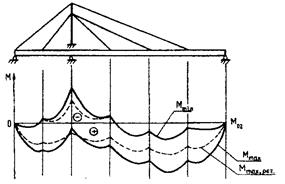
Рис. 13.5. Регулирование усилий в балке жесткости
Окончательные значения изгибающих моментов в балке складываются из трех составляющих: от постоянной нагрузки Мp, временной нагрузки Мv и от регулирования усилий Мpy.
В связи с тем, что на усилия в балке от постоянной нагрузки Мp значительно влияет способ монтажа, то выбор метода монтажа балки также может считаться фактором регулирования усилий (рис. 13.6).
При проектировании вантово-балочных мостов с регулированием усилий следует помнить о трех условиях:
1) на всех стадиях монтажа и регулирования конструкция должна оставаться геометрически неизменяемой с учетом того, что гибкие ванты могут работать только на растяжение;
2) усилия в вантах и балке жесткости на всех этапах не должны превышать предельных значений;
3) конструкция узлов должна предусматривать их двойное использование - во время регулирования усилий и в процессе эксплуатации.
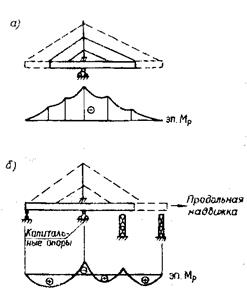
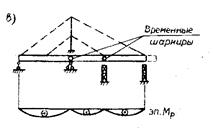
Рис. 13.6. Эпюры изгибающих моментов в балке жесткости от постоянной нагрузки Мp при монтаже:
а - навесным способом, б - методом продольной надвижки; в - с установкой временных шарниров
Одна из важнейших проблем - контроль за величиной регулирования усилий. В настоящее время используются три способа контроля:
1) по усилию в домкратах, которые выполняют предварительное натяжение;
2) по величине провисания середины ванты, которую предварительно маркируют;
3) по периоду собственных колебаний вант.
Более подробно вопросы регулирования усилий рассмотрены в работах [Вантовые мосты / А.А. Петропавловский, Е.И. Крыльцов, Н.Н. Богданов и др.; Под ред. А.А. Петропавловского. М.: Транспорт, 1985. 224 с., Перельмутер А.В. Основы расчета вантово-стержневых систем. М.: Стройиздат, 1969. 190 с.].
Практический расчет вантовых мостов на ЭВМ
Статический расчет вантовых мостов можно разделить на два этапа:
1) построение графиков внутренних усилий (М, N) и перемещений (h) аналогично рис. 13.7 и 13.8 при помощи различных программ для ЭВМ;
2) уточнение размеров поперечных сечений несущих элементов (вант, балки жесткости, пилонов) на основе их проверок по прочности, жесткости, выносливости.
Отсутствие эпюр поперечных сил в балке жесткости на рис. 13.7, 13.8 объясняется тем, что их величины в вантовых мостах весьма незначительны, и проверку по прочности по касательным напряжениям можно не проводить. Напомним, что ванты играют роль упругоподатливых опор, и эпюры поперечных сил имеют «пилообразный» вид.
На первом этапе статического расчета вантовых мостов рекомендуется использовать один из существующих сегодня вычислительных комплексов для ЭВМ (ЛИРА, PACK, РК, СПРИНТ, МКЭСС и т.д.).
На первом этапе статического расчета для построения графиков М, N, h (см. рис. 13.8) рекомендуется выполнить пять загружений моста (см. рис. 13.11). В отличие от висячих мостов балка жесткости вантовых конструкций воспринимает нагрузку от собственного веса. Но, учитывая то, что для большинства современных вантово-балочных мостов проводится регулирование усилий, более точные результаты для балки жесткости даст загружение моста только временной нагрузкой v (см. рис. 13.11, 13.12).
Первое загружение (v, h = l) позволяет определить максимальные усилия в балке Мi и Ni для главного пролета; второе загружение (v, h = l+l1) - Мi и Ni для боковых пролетов и минимальный отрицательный момент над опорным сечением Моп; третье загружение (v + р, h = l+l1) - максимальные усилия в вантах и пилоне Nв, i; четвертое загружение (v' + рн, h = l + l1) - экстремальные усилия в вантах для расчета на выносливость N'в,i; пятое загружение (vн, h = l) - экстремальные величины прогибов балки жесткости hi.
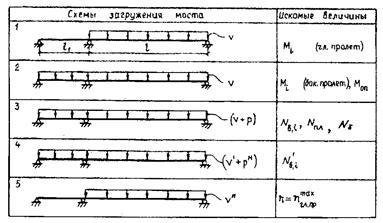
Рис. 13.11. Схемы загружения вантового моста для расчета на ЭВМ
При курсовом проектировании в случае, если приходится ограничиваться одним загружением, резонно выбрать первое загружение и получить все искомые экстремальные усилия и прогибы путем корректировки результатов с некоторым приближением (см. рис. 13.12).
Для вантовых мостов характерны относительно большие длины панелей di, поэтому их следует для расчета разбивать на 2-3 части.
После построения графиков (см. рис. 13.8) следует также дать оценку жесткости пролетного строения в целом:
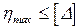 . (13.13)
. (13.13)
Если проверка (13.13) выполняется, то проводится подбор сечения балки и вант по прочности и выносливости по формулам (13.8), (13.9), (13.12), но с учетом того, что значения 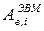 и
и 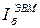 можно уменьшать только при наличии определенного запаса по жесткости (13.13).
можно уменьшать только при наличии определенного запаса по жесткости (13.13).
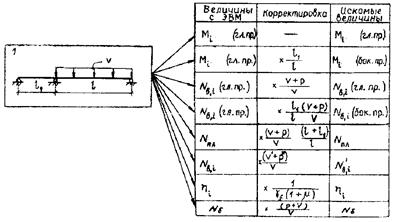
Рис. 13.12. Схема загружения вантового моста для получения приближенных результатов
При невыполнении условия (13.13) следует увеличить изгибную жесткость балки ЕIб и осевые жесткости вант ЕкАв,i пропорционально половине превышения hmax по сравнению с [D]:
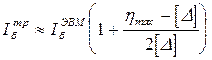 , (13.14)
, (13.14)
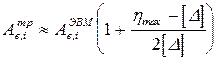 . (13.15)
. (13.15)
По найденным значениям 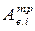 и
и 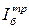 подбираются реальные сечения (Iб >
подбираются реальные сечения (Iб > 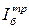 и Ав,i >
и Ав,i > 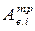 ), которые далее проверяются по прочности и выносливости. Аналогично проводится подбор сечения пилона по формуле (13.10). Однако следует иметь в виду, что у вантовых мостов часто используют одну плоскость вант и А-образные пилоны. Поэтому нужно четко следить за тем, с какой ширины пролетного строения собиралась нагрузка, на сколько плоскостей вант и стоек пилонов она передается.
), которые далее проверяются по прочности и выносливости. Аналогично проводится подбор сечения пилона по формуле (13.10). Однако следует иметь в виду, что у вантовых мостов часто используют одну плоскость вант и А-образные пилоны. Поэтому нужно четко следить за тем, с какой ширины пролетного строения собиралась нагрузка, на сколько плоскостей вант и стоек пилонов она передается.
Несколько больше отличий у вантовых мостов с железобетонной балкой жесткости. Для металлической балки проверка прочности выполняется по формуле (13.12). При этом необходимо помнить, что для вантовых мостов, в которых проводится регулирование усилий, можно считать, что изгибающие моменты в балке жесткости действуют только от нагрузки v - схемы № 1, 2 по рис. 13.11. Но продольные силы в балке возникают от суммарной нагрузки (v + р) - схема 3, рис. 13.11, что необходимо учитывать при подстановке величин Nб и Мб в формулу (13.12).
Для железобетонной балки тоже допускается проводить проверку прочности как для упругого тела (формула (13.12), но без коэффициентов y, c, m и с заменой Ry на Rbt), если она подбиралась из условия обеспечения жесткости пролетного строения (13.14) и напряжения в ней sб, значительно меньше расчетного Rbt. Но если балка работает со значительными напряжениями sб, то ее сечение следует проверить по методике предельных состояний, предварительно расставив арматуру.
Рассмотренный ранее вопрос учета провисания вант под действием собственного веса (см. рис. 13.1, д) требует итерационного процесса. Необходимо выполнить несколько уточняющих перерасчетов конструкции с изменением модуля упругости вант на каждой стадии итерации, определяя приведенный модуль упругости Еef по формуле (195) СНиП.
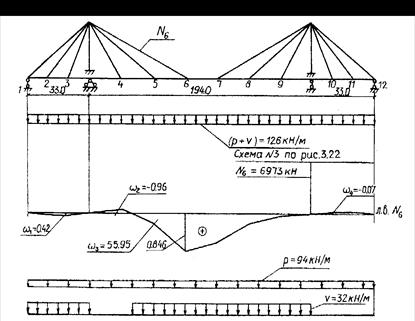
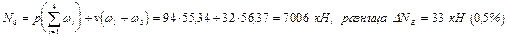
Рис. 13.13. Пример загружения вантового моста по схеме рис. 13.11 с невыгодным
положением временной нагрузки в соответствии с линией влияния
Алгоритм загружения висячих и вантовых мостов, представленный на рис. 13.9-13.12 для более точных расчетов, например при дипломном проектировании, можно дополнить построением линий влияния. Современные вычислительные комплексы позволяют это сделать с минимальными затратами.
Как отмечалось ранее, аппарат линий влияния применим для получения невыгодных загружений временной подвижной нагрузкой для вантовых и висячих мостов, хотя для последних с некоторым приближением. На рис. 13.13 показан пример уточнения схемы загружения постоянной и временной нагрузками для получения экстремальных усилий в ванте N6 по линии влияния.
3. Подготовка исходных данных для расчета на ЭВМ.В настоящее время в учебных целях широко используется вычислительный комплекс на основе МКЭ, разработанный в МГТУПС под руководством проф. Н.Н. Шапошникова. Ниже приводятся рекомендации по подготовке исходных данных применительно к данной программе, хотя они могут быть использованы и для других вычислительных комплексов.
Прежде всего, следует учесть гибкость вант, кабеля и подвесок путем задания их малой изгибной жесткости (I » 0,000001 м4). Для исключения проблем с размерностью все усилия рекомендуется задавать в килоньютонах, геометрические размеры в метрах, а модули упругости в килоньютонах на метр в квадрате (Es = 2·108 кН/м2, Еb = 0,3·108 кН/м2).
Нумерация узлов и стержней выполняется сначала по балке жесткости, потом по участкам кабеля, подвескам или вантам, пилонам, таким образом, чтобы можно было для ввода исходных данных использовать сервисную опцию «Повторитель» (рис. 13.14, 13.15). Для висячих мостов можно в расчетной схеме уменьшить количество подвесок для сокращения числа узлов и стержней. При этом следует помнить, что увеличение шага подвесок в 2...4 раза требует при задании их жесткости в такое же число раз увеличить площадь их поперечного сечения.
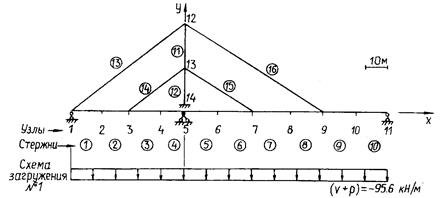
На рис. 13.14 и 13.15 приведены численные примеры подготовки исходных данных для вантового и висячего мостов. Для вантовой схемы панели балки жесткости желательно разделить на 2-3 части, чтобы получить более точное очертание эпюр внутренних усилий (см. рис. 13.14).
| Стержни | |||||||||
| № | начало | x | у | шарнир | конец | x | у | шарнир | сечение |
| -50.0 | 0.0 | -37.5 | 0.0 | ||||||
| -37.5 | 0.0 | -25.0 | 0.0 | ||||||
| -25.0 | 0.0 | -12.5 | 0.0 | ||||||
| -12.5 | 0.0 | 0.0 | 0.0 | ||||||
| 0.0 | 0.0 | 15.0 | 0.0 | ||||||
| 15.0 | 0.0 | 30.0 | 0.0 | ||||||
| 30.0 | 0.0 | 45.0 | 0.0 | ||||||
| 45.0 | 0.0 | 60.0 | 0.0 | ||||||
| 60.0 | 0.0 | 75.0 | 0.0 | ||||||
| 75.0 | 0.0 | 90.0 | 0.0 | ||||||
| 0.0 | 40.0 | 0.0 | 20.0 | ||||||
| 0.0 | 20.0 | 0.0 | 1.0 | ||||||
| -50.0 | 0.0 | 0.0 | 40.0 | ||||||
| -25.0 | 0.0 | 0.0 | 20.0 | ||||||
| 30.0 | 0.0 | 0.0 | 20.0 | ||||||
| 60.0 | 0.0 | 0.0 | 40.0 |
| Сечения | |||
| № | E | F(A) | I |
| 2D+8 | 0.5 | 0.1 | |
| 0.37D+8 | 0.8 | 0.07 | |
| 1.7D+8 | 0.05 | 1D-7 | |
| №1 | Eб = 2*108 кН/м2, |
| Аб = 0,5 м2, | |
| Iб = 0,1 м4; | |
| №2 | Eпл = 0,37*108 кН/м2, |
| Апл = 0,8 м2, | |
| Iпл = 0,07 м4; | |
| №3 | Eк = 1,7*108 кН/м2, |
| Ав = 0,05 м2, | |
| Iв = 0,000001 м4. |
| Узлы | ||||||
| № | x | y | опора | шарнир | направление | |
| -50.0 | 0.0 | |||||
| -37.5 | 0.0 | |||||
| -25.0 | 0.0 | |||||
| -12.5 | 0.0 | |||||
| 0.0 | 0.0 | |||||
| 15.0 | 0.0 | |||||
| 30.0 | 0.0 | |||||
| 45.0 | 0.0 | |||||
| 60.0 | 0.0 | |||||
| 75.0 | 0.0 | |||||
| 90.0 | 0.0 | |||||
| 0.0 | 40.0 | |||||
| 0.0 | 20.0 | |||||
| 0.0 | 1.0 |
| Распределенные силы | |||||
| № | вид нагрузки | стержни | направление | значение (начало) | значение (конец) |
| 1 загруж. | 2 по у | -95.6 | -95.6 | ||
| 1 загруж. | 2 по у | -95.6 | -95.6 | ||
| 1 загруж. | 2 no у | -95.6 | -95.6 | ||
| 1 загруж. | 2 по у | -95.6 | -95.6 | ||
| 1 загруж. | 2 по у | -95.6 | -95.6 | ||
| 1 загруж. | 2 по у | -95.6 | -95.6 | ||
| 1 загруж. | 2 по у | -95.6 | -95.6 | ||
| 1 загруж. | 2 по у | -95.6 | -95.6 | ||
| 1 загруж. | 2 по у | -95.6 | -95.6 | ||
| 1 загруж. | 2 по у | -95.6 | -95.6 |
| Рис. 13.14. Пример подготовки исходных данных для расчета вантового моста методом конечных элементов |
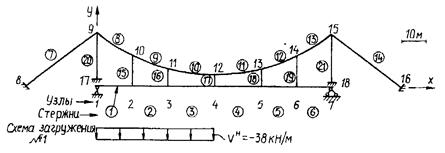
| Es= 2*108 кН/м2 | Eк = 1,5*108 кН/м2 | Iб = 0.2 м4 | Аб = 0.5 м2 |
| Ак = 0.1 м2 | Апл = 0.01 м2 | Апл = 0.3 м2 | Iпл = 0.03 м4 |
|
|
| Рис. 13.15. Пример подготовки исходных данных для расчета висячего моста методом конечных элементов |
| Сечения | |||
| № | E | F(A) | I |
| 2D+8 | 0.5 | 0.2 | |
| 1.5D+8 | 0.1 | 1D-7 | |
| 1.5D+8 | 0.01 | 1D-7 | |
| 0.37D+8 | 0.3 | 0.03 |
| <== предыдущая лекция | | | следующая лекция ==> |
| Теоретические основы расчета висячих мостов | | | Динамические и аэродинамические расчеты висячих и вантовых мостов |
Дата добавления: 2021-06-28; просмотров: 1448;











