Стандартные аксонометрические системы

Из частных видов аксонометрических проекций, предусмотренных государственным стандартом, чаще всего используют ортогональную изометрию, и ортогональную диметрию.

Ортогональная изометрия. В изометрии показатели искажения по всем трём осям одинаковы, т.е. p=q=r. Аксонометрические оси в ортогональной изометрии образуют между собой углы по 120º (рисунок 2.2.1).

В ортогональной изометрии 3р²=2 или p=q=r=0,82. На практике для удобства построения пользуются приведённой ортогональной изометрией, в которой показатели искажения приводятся к единице, т.е. p=q=r=1. При этом коэффициент приведения будет равен m=1/p=1,22. Это означает, что приведённая ортогональная изометрия даёт увеличение изображения приблизительно в 1,22 раза, т.е. масштаб такого изображения будет M 1,22:1.

Рисунок 2.2.1 – Оси ортогональной изометрии

Ортогональная диметрия. В то время, как ортогональная изометрия существует только одна, ортогональных диметрий можно построить бесчисленное множество. Наиболее простую и распространённую диметрию получают, если p=r и q=p/2.

В ортогональной диметрии 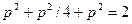, откуда

Тогда p=r=0,94; q=0,47.

В приведённой ортогональной диметрии показатели искажения будут p=r=1 и q=0,5. При этом коэффициент приведения равен: m=1/p=1,06.

Это означает, что приведённая ортогональная диметрия даёт изображение в масштабе М 1,06:1. Расположение осей определяется с помощью тангенсов углов наклона осей к горизонтальной линии. Практически можно использовать следующий способ построения аксонометрических осей в ортогональной диметрии (рисунок 2.2.2).

Рисунок 2.2.2 – Оси ортогональной диметрии

Через точку О¢ проводим вспомогательную прямую, перпендикулярную к выбранной оси z¢. В обе стороны от точки О¢ откладываем на этой прямой по восемь произвольных, но равных между собой отрезков. В направлении, противоположном положительному направлению оси z¢, откладываем от левой конечной точки один такой же отрезок, а от правой конечной точки – семь отрезков. Соединив полученные точки с точкой О¢, получим аксонометрические оси x¢ и y¢.