Способ замены плоскостей проекций

Отличительная особенность способа замены плоскостей проекций состоит в переходе от данной системы плоскостей, в которой заданы проекции объекта, к новой системе двух взаимно перпендикулярных плоскостей. Положение самого объекта в пространстве остаётся неизменным.

Замена плоскостей проекций осуществляется последовательно.

Рассмотрим замену одной плоскости проекций. Пусть дана одна пара плоскостей проекций П₁ и П₂ (рисунок 1.4.1).

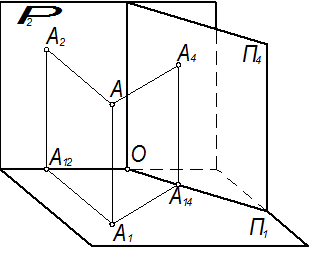
Рисунок 1.4.1 – Замена фронтальной плоскости проекций

Спроецируем какую-либо точку А на эти плоскости и определим её проекции А₁ и А₂. Возьмём новую плоскость проекций П₄, перпендикулярную к плоскости П₁, и спроецируем точку А на эту плоскость, обозначив полученную проекцию А₄. Как видно из рисунка 1.4.1, пара А₁ и А₄ при заданном положении плоскостей проекций П₁ и П₄ определяет в пространстве точку А.

Таким образом, мы имеем проекции точки А в старой системе (П₁, П₄) и её проекции в новой системе (П₁, П₄).

Очевидно, что обе системы абсолютно равноправны (обе фронтальные плоскости П₂ и П₄ перпендикулярны к П₁). Поэтому свойства, установленные ранее для системы (П₁, П₂) можно полностью перенести на систему (П₁, П₄). Чтобы от чертежа, выполненного в старой системе, перейти к чертежу, выполненному в новой системе, надо установить, какие из свойств остаются инвариантными (неизменными) при таком переходе от старой системы к новой. Очевидно, это будут те свойства проекций, которые связаны лишь с неподвижной плоскостью П₁, т.е. остаются неизменными:

1) горизонтальная проекция А₁ точки А;

2) высота точки А: А₁А=А₁₂А₂=А₁₄А₄₌h^А.

Аналогично можно заменить горизонтальную плоскость проекций П₁ новой плоскостью П₅, которая перпендикулярна остающейся плоскости проекций П₂ в соответствии с рисунком 1.4.2. При этом мы имеем проекции точки В (В₁, В₂) в старой системе (П₁, П₂) и её проекции в новой системе В(В₂, В₅) в новой системе (П₂, П₅). В этом случае остаются неизменными следующие свойства проекций:

1) фронтальная проекция В₂ точки В;

2) глубина точки В: В₂В=В₁₂В₁= В₂₅В₅=v^B.

На рисунке 1.4.3 показана операция перехода от системы (П₁, П₂) к системе (П₁, П₄) на комплексном чертеже.

Проведём новую ось х₁₄ и построим точку А₁₄, опуская перпендикуляр из точки А₁ на ось х₁₄. На этом перпендикуляре откладываем отрезок А₁₄А₄=А₁₂А₂=h^А. Полученная таким образом точка А₄ является проекцией точки А на плоскость П₄. О₁₂₄ – точка, у которой все три проекции совпадают.

Операция перехода от системы (П₁, П₂) к системе (П₂, П₅) на комплексном чертеже показана на рисунке 1.4.4. Линия связи В₂В₅ перпендикулярна к новой оси х₂₅.

Рисунок 1.4.2 – Замена горизонтальной плоскости проекций

Рисунок 1.4.3 – Замена фронтальной плоскости проекций

на комплексном чертеже

Рисунок 1.4.4 – Замена горизонтальной плоскости проекций

на комплексном чертеже

Рассмотрим замену двух плоскостей проекций в соответствии с рисунком 1.4.5.

Построения, выполняемые при последовательной замене двух плоскостей проекций, принципиально ничем не отличаются от тех, которые делались при однократной замене. При этом надо руководствоваться общим правилом: расстояния новых проекций точек от новой оси равны расстояниям заменяемых проекций от предыдущей оси.

Рисунок 1.4.5 – Замена двух плоскостей проекций на комплексном чертеже