Пересечение поверхности с плоскостью

Это есть позиционная задача на определение для данных геометрических объектов их общего элемента, которым является кривая линия.

Для её построения используются вспомогательные плоскости-посредники частного положения, одновременно пересекающие данные поверхность и плоскость.

Построение линии b пересечения фронтально проецирующей плоскости Q с поверхностью закрытого тора выполнено в соответствии с рисунком 1.3.48. Для этого введён ряд вспомогательных горизонтальных плоскостей –посредников Г(Г₂), Г¢(Г¢₂), Г¢(Г¢₂) и т.д. Плоскость Г(Г₂) пересекает поверхность закрытого тора по окружностям l(l₁,l₂), а плоскость Q она пересекает по фронтально проецирующей прямой (3-3¢). Проекции этой прямой на чертеже обозначены следующим образом: горизонтальная – (3₁-3¢₁) и фронтальная – (3₂º3¢₂). Точки 3 и 3¢ в силу проецирующего положения плоскости Q являются одновременно и точками линии b как линии пересечения плоскости Q с данной поверхностью закрытого тора. Все другие точки линии b определяются аналогично точкам 3 и 3¢ при помощи плоскостей-посредников Г¢, Г¢ и т.д. Проекции линии b на чертеже обозначены следующим образом: фронтальная – b₂ºQ₂ и горизонтальная – b₁, представляющая собой плавную кривую, соединяющую точки 3, 3¢ и т.д. Следует заметить, что при построении линии b в первую очередь надо отметить точки 1 и 2 как опорные. Положение этих точек при данном расположении на чертеже поверхности закрытого тора и плоскости Q определяется наличием общей плоскости симметрии S(S₁), которая является плоскостью главного меридиана поверхности закрытого тора. Действительно, плоскостью симметрии плоскости Q(Q₂) будет вообще любая плоскость, к ней перпендикулярная, а плоскостью симметрии поверхности будет всякая плоскость, проходящая через её ось. Общая плоскость симметрии должна удовлетворять обоим указанным условиям и очевидно, что такой плоскостью будет S(S₁). В силу этого линия b тоже симметрична относительно плоскости S, а её горизонтальная проекция симметрична относительно следа плоскости S₁. Точки 1 и 2 лежат на главном меридиане поверхности. Отметив их фронтальные проекции 1₂ и 2₂, найдём горизонтальные проекции этих точек (1₁ и 2₁) на горизонтальной проекции главного меридиана.

Построение линии пересечения гранной поверхности с плоскостью выполнено в соответствии с рисунком 1.3.49.

Сечение многогранника может быть ограничено только отрезками прямых. Число сторон такого многогранника равно числу граней многогранника, пересекаемых плоскостью. Вершинами многоугольника сечения являются точки пересечения рёбер многогранника с секущей плоскостью. Следовательно, число вершин многоугольника равно числу рёбер многогранника, пересекаемых плоскостью.

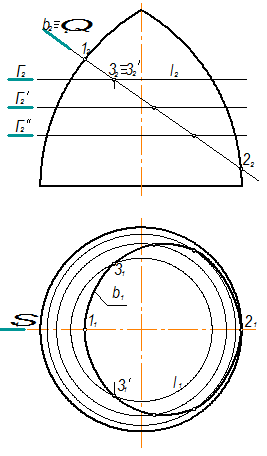
Рисунок 1.3.48 – Пересечение плоскости с поверхностью закрытого тора

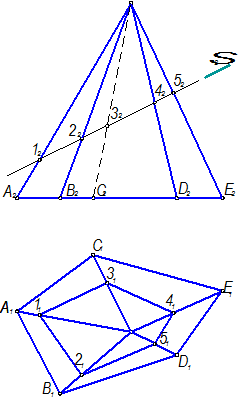
Рисунок 1.3.49 – Пересечение гранной поверхности с плоскостью

Следует заметить, что вершинами многоугольника сечения являются точки пересечения секущей плоскости с рёбрами многогранника в собственном смысле. Это значит, что точки пересечения секущей плоскости с продолжением рёбер не могут являться вершинами многоугольника сечения как не принадлежащие поверхности многогранника, но могут быть использованы для удобства построения.

Аналогично, сторонами многоугольника сечения могут являться только те отрезки прямых, которые принадлежат граням в собственном смысле.

В данном примере пирамида пересекается с фронтально проецирующей плоскостью S(S₁). Решение получается простым, поскольку фронтальная проекция сечения вырождается в отрезок прямой линии, совпадающей с фронтальным следом плоскости S. Горизонтальной проекцией сечения является пятиугольник с вершинами 1₁, 2₁, 4₁, 5₁, 3₁.

Конические сечения

Линии, которые получаются при пересечении поверхности конуса второго порядка с плоскостью, называются коническими сечениями.

К этим линиям относятся следующие: эллипс,парабола,гипербола,окружность,две прямые.

Рассмотрим, при каких условиях получается то или иное сечение на примере пересечения конуса второго порядка проецирующей плоскостью (рисунок 1.3.50).

Рисунок 1.3.50 – Конические сечения

Если секущая плоскость S¹(S¹₂) пересекает все образующие конуса, то в сечении получается эллипс.

Если секущая плоскость S(S₂) перпендикулярна к оси вращения конуса, то в сечении получается окружность.

Если секущая плоскость S²(S²₂) параллельна одной образующей конуса, то в сечении будет парабола.

Если секущая плоскость S³(S³₂) параллельна двум образующим конуса, то получим гиперболу.

Гипербола может быть получена и в случае расположения секущей плоскости S⁴(S⁴₂) параллельно оси конуса. В этом случае плоскость параллельна двум образующим, проекции которых совпадают с проекцией оси.

Две прямые в сечении получаются, если секущая плоскость S⁵(S⁵₂) проходит через вершину конуса.

Пример построения сечения конуса по параболе показан на рисунке 2.3.51. При построении сначала определялись опорные (экстремальные) точки 1, 2, и 2¢. Затем определялись промежуточные точки с помощью горизонтальных плоскостей-посредников Г(Г₂). Их построение можно видеть на примере точек 3 и 3¢.

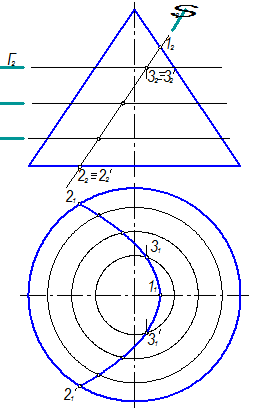
Рисунок 1.3.51 – Сечение конуса по параболе